搜索
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)
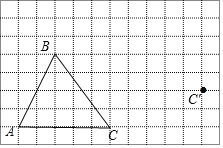
(1)画出平移后的△A′B′C′.
(2)画出AB边上的中线线CD；
(3)在整个平移过程中，线段BC扫过的面积是___.
参考答案：
【答案】（1）如图所示；（2）如图所示；（3）26.
【解析】
（1）根据C′位置结合网格特点和平移的性质，可得A′，B′的位置，然后顺次连接即可；
（2）找到AB边上的中点D，连接CD即可；
（3）用平行四边形BCC′B′所在矩形的面积减去周围四个直角三角形的面积即可.
解：（1）如图所示，△A′B′C′即为所求；
（2）如图所示，CD即为所求；
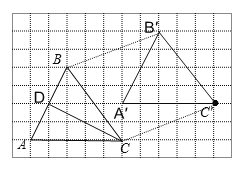
（3）线段BC扫过的面积=8×6-
×2×5-×3×4-×2×5-×3×4=26.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（14分）如图，已知抛物线
（
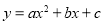）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．
（1）求此抛物线的解析式；
（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；
（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，O为坐标原点，点A的坐标为（a,a），点B的坐标（b,c），且a、b、c满足
.(1)若a没有平方根，判断点A在第几象限并说明理由.
(2)连AB、OA、OB，若△OAB的面积大于5而小于8，求a的取值范围；
(3)若两个动点M（2m,3m-5），N(n-1,-2n-3)，请你探索是否存在以两个动点M、N为端点的线段MN∥AB，且MN=AB.若存在，求出M、N两点的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在正方形
外取一点
，连接
、
、
．过点
作的垂线交于点
．若
，
．下列结论：①
；②点
到直线的距离为
；③
；④
；⑤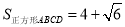
；其中正确结论的序号是( )
A.①③④B.①②⑤C.③④⑤D.①③⑤
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次数学兴趣小组活动中，同学们做了一个找朋友的游戏：有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面，如图，A、B、C、D、E、F所持的纸牌的前面分别写有六个算式：66；63+63；（63）3；（2×62）×（3×63）；（22×32）3；（64）3÷62．游戏规定：所持算式的值相等的两个人是朋友．如果现在由同学A来找他的朋友，他可以找谁呢？说说你的看法．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为宣传6月6日世界海洋日，某校八年级举行了主题为“珍惜海洋资源，保护海洋生物多样性”的知识竞赛活动．为了解全年级500名学生此次竞赛成绩(百分制)的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如下不完整的统计表(表1)和统计图(如图)．请根据图表信息解答以下问题：
（1）本次调查一共随机抽取了个参赛学生的成绩；
（2）表1中a＝ ；
（3）所抽取的参赛学生的成绩的中位数落在的“组别”是 ；
（4）请你估计，该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE、DF、EF，则添加下列哪一个条件后，仍无法判断△FCE与△EDF全等（ ）
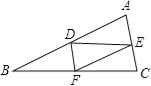
A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
相关试题
