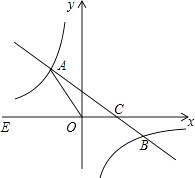
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 ![]() 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=
的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= ![]() .
. 
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数值时自变量x的取值范围.
参考答案:
【答案】
(1)解:作AD⊥x轴于D,如图,
在Rt△OAD中,∵sin∠AOD= ![]() =
= ![]() ,
,
∴AD= ![]() OA=4,
OA=4,
∴OD= ![]() =3,
=3,
∴A(﹣3,4),
把A(﹣3,4)代入y= ![]() 得m=﹣4×3=﹣12,
得m=﹣4×3=﹣12,
所以反比例函数解析式为y=﹣ ![]() ;
;
把B(6,n)代入y=﹣ ![]() 得6n=﹣12,解得n=﹣2,
得6n=﹣12,解得n=﹣2,
把A(﹣3,4)、B(6,﹣2)分别代入y=kx+b得 ![]() ,解得
,解得  ,
,
所以一次函数解析式为y=﹣ ![]() x+2;
x+2;
(2)当y=0时,﹣ ![]() x+2=0,解得x=3,则C(3,0),
x+2=0,解得x=3,则C(3,0),
所以S△AOC= ![]() ×4×3=6;
×4×3=6;
(3)解:当x<﹣3或0<x<6时,一次函数的值大于反比例函数的值.

【解析】(1)作AD⊥x轴于D,如图,先利用解直角三角形确定A(﹣3,4),再把A点坐标代入y= ![]() 可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是____cm2.
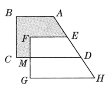
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB、BC、AC三边的长分别为
 ,
,  ,
,  ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为
 ,
,  ,
,  ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .(3)在△ABC中,AB=2
 ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
-
科目: 来源: 题型:
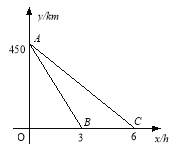
查看答案和解析>>【题目】(本题满分8分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速
运动.快车离乙地的路程y1 (km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路
程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图像进行以下研究.
解读信息:(1)甲、乙两地之间的距离为 km;
(2)线段AB的解析式为 ; 两车在慢车出发 小时后相遇;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图像.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
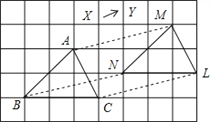
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
相关试题

