搜索
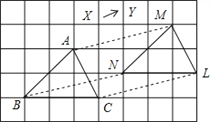
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有（ ）
①AM∥BN；②AM=BN；③BC=ML；④∠ACB=∠MNL。
A. 1个 B. 2个 C. 3个 D. 4个
参考答案：
【答案】B
【解析】分析：如图，由△ABC平移得到△MNL可知A与M、B与N、C与L是对应点，根据平移的特征得：AM∥BN∥CL且AM=BN=CL，△ABC与△MNL的形状、大小完全相同.从而进行判断即可.
详解：根据平移前后连接对应点的线段平行且相等可知：
①AM∥BN正确，②AM=BN正确；
根据平移前后△ABC与△MNL的形状、大小完全相同可知
BC=NL、∠ACB=∠MLN，所以：③BC=ML错误，④∠ACB=∠MNL错误.
故选B.
-
科目： 来源： 题型：
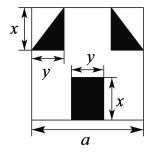
查看答案和解析>>【题目】“囧”像一个人脸郁闷的神情．如图，边长为a的正方形纸片，剪去两个一样的小直角三角形（阴影部分）和一个长方形（阴影部分）得到一个“囧”字图案，设剪去的两个小直角三角形的两直角边长分别为x、y，剪去的小长方形长和宽也分别为x，y．
（1）用含a、x、y的式子表示“囧”的面积；
（2）当a=12，x=7，y=4时，求该图形面积的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设a1=22－02，a2=32－12，…，an=(n+1)2－(n－1)2（n为大于1的整数）
（1）计算a15的值；
（2）通过拼图你发现前三个图形的面积之和与第四个正方形的面积之间有什么关系：
__________________________________（用含a、b的式子表示）；
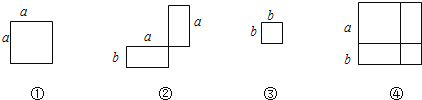
（3）根据(2)中结论，探究an=(n+1)2－(n－1)2是否为4的倍数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：c=10，且a，b满足(a+26)2+|b+c|=0，请回答问题：
（1）请直接写出a，b，c的值：a= ，b= ；
（2）在数轴上a、b、c所对应的点分别为A、B、C，记A、B两点间的距离为AB，则AB= ，AC= ；
（3）在（1）（2）的条件下，若点M从点A出发，以每秒1个单位长度的速度向右运动，当点M到达点C时，点M停止；当点M运动到点B时，点N从点A出发，以每秒3个单位长度向右运动，点N到达点C后，再立即以同样的速度返回，当点N到达点A时，点N停止．从点M开始运动时起，至点M、N均停止运动为止，设时间为t秒，请用含t的代数式表示M，N两点间的距离．
-
科目： 来源： 题型：
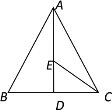
查看答案和解析>>【题目】如图所示，在等边三角形ABC中，BC边上的高AD＝10，E是AD上一点，现有一动点P沿着折线A－E－C运动，在AE上的速度是4单位/秒，在CE上的速度是2单位/秒，则点P从A到C的运动过程中至少需_______秒．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.
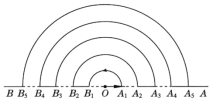
A. 5050π B. 5050π+101 C. 5055π D. 5055π+101
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD为正方形，AB=2
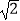，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．
（1）求证：矩形DEFG是正方形；
（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由；
（3）设AE=x，四边形DEFG的面积为S，求出S与x的函数关系式．
相关试题
