【题目】(本题满分8分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速
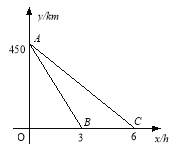
运动.快车离乙地的路程y1 (km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路
程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图像进行以下研究.
解读信息:(1)甲、乙两地之间的距离为 km;
(2)线段AB的解析式为 ; 两车在慢车出发 小时后相遇;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图像.
参考答案:
【答案】(1)甲、乙两地之间的距离为 450 km;
(2)线段AB的解析式为 y1=450-150 x (0≤x≤3); 两车在慢车出发 2 小时后相遇;
(3)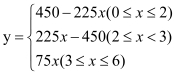
其图象为折线图

拐点处的数据一定要标出,若未标出,扣分。
【解析】
试题(1)根据图像中点A的坐标可知甲、乙两地之间的距离为 450km;(2)线段AB的解析式为y=kx+b把点A(0,450),B(3,0)代入y=kx+b,然后解方程组即可,根据图象可求出快车的速度![]() 千米/小时,是慢车的速度是
千米/小时,是慢车的速度是![]() 千米/小时,所以两车在慢车出发
千米/小时,所以两车在慢车出发![]() 小时后相遇;(3)分三种情况讨论:
小时后相遇;(3)分三种情况讨论:![]() 即可.
即可.
试题解析:(1)根据图像中点A的坐标可知甲、乙两地之间的距离为 450km;(2)线段AB的解析式为y=kx+b把点A(0,450),B(3,0)代入y=kx+b得![]() 解得
解得![]() ,所以y1=450-150 x (0≤x≤3),根据图象可求出快车的速度
,所以y1=450-150 x (0≤x≤3),根据图象可求出快车的速度![]() 千米/小时,是慢车的速度是
千米/小时,是慢车的速度是![]() 千米/小时,所以两车在慢车出发
千米/小时,所以两车在慢车出发![]() 小时后相遇;(3)分三种情况讨论:当
小时后相遇;(3)分三种情况讨论:当![]() 时,y=450-225x,当
时,y=450-225x,当![]() 时,y=225x-450,当
时,y=225x-450,当![]() 时,y=75x,所以
时,y=75x,所以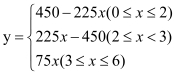 ,其图象为折线图
,其图象为折线图

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB、BC、AC三边的长分别为
 ,
,  ,
,  ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为
 ,
,  ,
,  ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .(3)在△ABC中,AB=2
 ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
-
科目: 来源: 题型:
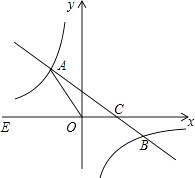
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数
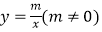 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=
的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=  .
. 
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数值时自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
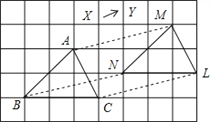
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
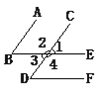
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
相关试题

