【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )
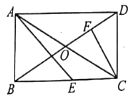
A. ①②B. ②③C. ①②④D. ①②③
参考答案:
【答案】D
【解析】
根据矩形的性质,由∠ADB=30°可得,△AOB和△COD都是等边三角形,再由∠AEB=45°,可得△ABE是等腰直角三角形,其边有特殊的关系,利用等量代换可以得出③AE=![]() AO是正确的,①BE=CD是正确的,在正△COD中,CF⊥BD,可得DF=
AO是正确的,①BE=CD是正确的,在正△COD中,CF⊥BD,可得DF=![]() CD,再利用等量代换可得②BF=3DF是正确的,利用选项的排除法确定选项D是正确的.
CD,再利用等量代换可得②BF=3DF是正确的,利用选项的排除法确定选项D是正确的.
解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AC=BD,AO=CO=BO=DO,∠ABC=∠ADC=∠BAD=∠BCD=90°,
∵∠AEB=45°,
∴∠BAE=∠AEB=45°
∴AB=BE=CD,AE=![]() AB=
AB=![]() CD,
CD,
故①正确,
∵∠ADB=30°,
∴∠ABO=60°且AO=BO,
∴△ABO是等边三角形,
∴AB=AO,
∴AE=![]() AO,
AO,
故③正确,
∵△OCD是等边三角形,CF⊥BD,
∴DF=FO=![]() OD=
OD=![]() CD=
CD=![]() BD,
BD,
∴BF=3DF,
故②正确,
根据排除法,可得选项D正确,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 城气象台测得台风中心在
城气象台测得台风中心在 城正西方向
城正西方向 的
的 处,以每小时
处,以每小时 的速度向南偏东
的速度向南偏东 的
的 方向移动,距台风中心
方向移动,距台风中心 的范围内是受台风影响的区域.
的范围内是受台风影响的区域.
(1)求
 城与台风中心之间的最小距离;(2)求
城与台风中心之间的最小距离;(2)求 城受台风影响的时间有多长?
城受台风影响的时间有多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级全体同学参加了学校捐款活动,随机抽取了部分同学捐款的情况统计图如图所示
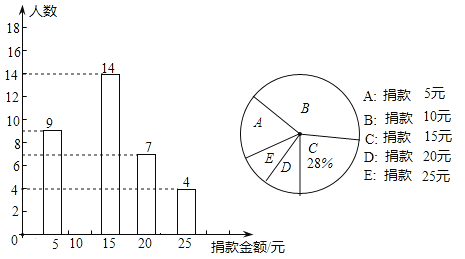
(1)本次共抽查学生 人,并将条形统计图补充完整;
(2)捐款金额的众数是 ,中位数是 ;
(3)在八年级600名学生中,捐款20元及以上的学生估计有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
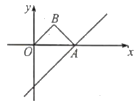
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x之间的函数解析式.
(2)在所给直角坐标系中画出函数图象.
(3)由函数图象直接写出当﹣2≤y≤2时,自变量x的取值范围.

相关试题

