【题目】如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
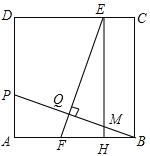
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段AF的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)先根据EQ⊥BO,EH⊥AB得出∠EQN=∠BHM=90°.根据∠EMQ=∠BMH得出△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得出△APB≌△HFE,故可得出结论;
(2)由勾股定理求出BP的长,根据EF是BP的垂直平分线可知BQ=![]() BP,再根据锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=4
BP,再根据锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=4![]() ,再根据EQ=EF-QF即可得出结论.
,再根据EQ=EF-QF即可得出结论.
试题解析:(1)∵EQ⊥BO,EH⊥AB,
∴∠EQN=∠BHM=90°.
∵∠EMQ=∠BMH,
∴△EMQ∽△BMH,
∴∠QEM=∠HBM.
在Rt△APB与Rt△HFE中,
![]() ,
,
∴△APB≌△HFE,
∴HF=AP;
(2)由勾股定理得,BP=![]() .
.
∵EF是BP的垂直平分线,
∴BQ=![]() BP=2
BP=2![]() ,
,
∴QF=BQtan∠FBQ=BQtan∠ABP=2![]() ×
×![]() =
=![]() .
.
由(1)知,△APB≌△HFE,
∴EF=BP=4![]() ,
,
∴EQ=EF-QF=4![]() -
-![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对一大型超市销售的甲、乙、丙3 种大米进行质量检测.共抽查大米200袋,质量评定分为 A、B两个等级(A级优于B级),相应数据的统计图如下:
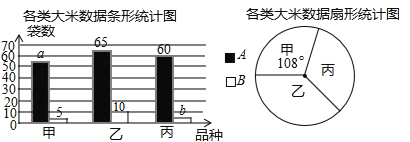
根据所给信息,解决下列问题:
⑴①该次调查的样本容量是 ; ②a= ,b= ;
⑵已知该超市现有乙种大米750 袋,根据检测结果,请你估计该超市乙种大米中有多少袋 B级大米?
⑶对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线经过
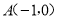 ,
,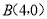
 ,⊙M是△ABC的外接圆,M为圆心.
,⊙M是△ABC的外接圆,M为圆心.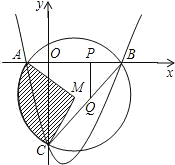
(1)求抛物线的解析式;
(2)求阴影部分的面积;
(3)在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=k,△CPQ的面积为S,求S关于k的函数关系式,并求出S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线相交于点O,那么下列说法不正确的是( )
A. 点O一定在△ABC的内部 B. ∠D的平分线一定经过点O
C. 点O到△ABC三边的距离一定相等 D. 点O到△ABC的三个顶点的距离一定相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x-25=_____.
相关试题

