【题目】如图,在平面直角坐标系中,抛物线经过![]() ,
,![]()
![]() ,⊙M是△ABC的外接圆,M为圆心.
,⊙M是△ABC的外接圆,M为圆心.
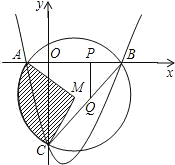
(1)求抛物线的解析式;
(2)求阴影部分的面积;
(3)在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=k,△CPQ的面积为S,求S关于k的函数关系式,并求出S的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
试题分析:
(1)已知了A、B、C三点坐标可用待定系数法求出抛物线的解析式.
(2)要求扇形的面积需要知道半径的长和扇形的圆心角的度数,先求圆心角∠AMC的度数,由于OB=OC,因此∠ABC=45°,根据圆周角定理可得出∠AMC=90°.再求半径,由于三角形AMC是等腰直角三角形,因此半径的平方等于AC的平方的一半,可在直角三角形OAC中求出AC的平方,据此可根据扇形的面积公式求出扇形的面积.
(3)求三角形CPQ的面积可以PQ为底,以OP为高,已知了PQ=k,在等腰直角三角形BPQ中,BP=PQ=k,也就能表示长OP的长,据此可求出S与k的函数关系,根据函数的性质即可求出S的最大值.
试题解析:
解:(1)由抛物线经过![]() ,
,
设抛物线的解析式为:![]() ,
,
将![]() 代入上式中,得
代入上式中,得![]() .
.
∴![]() .
.
(2)∵![]() .
.
∴![]()
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]() .
.
(3)![]() ,
,![]() 轴;
轴;
∴![]() ,
,
∴![]() .
.
∴当![]() 时,
时,![]() .
.
考点: 二次函数综合题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简(a2b-2ab2-b3)÷b-(a+b)(a-b),然后对式子中a、b分别选择一个自己最喜欢的数代入求值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
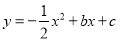 与坐标轴分别交于点
与坐标轴分别交于点 和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.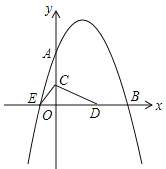
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对一大型超市销售的甲、乙、丙3 种大米进行质量检测.共抽查大米200袋,质量评定分为 A、B两个等级(A级优于B级),相应数据的统计图如下:
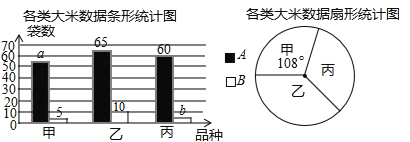
根据所给信息,解决下列问题:
⑴①该次调查的样本容量是 ; ②a= ,b= ;
⑵已知该超市现有乙种大米750 袋,根据检测结果,请你估计该超市乙种大米中有多少袋 B级大米?
⑶对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
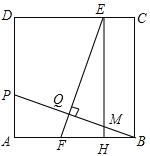
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
相关试题

