Question

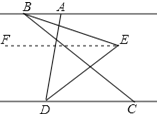
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.

(1)求∠EDC的度数;

(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);

(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

Answer 1

【答案】（1）35°.；（2）n°+35°.（3）215°-n°.

【解析】试题分析：（1）、根据角平分线直接得出答案；（2）、过点E作EF∥AB，然后根据平行线的性质和角平分线的性质求出角度；（3）、首先根据题意画出图形，然后过点E作EF∥AB，按照第二小题同样的方法进行计算角度.

试题解析：（1）、∵DE平分∠ADC，∠ADC=70°，

∴∠EDC=∠ADC=×70°=35°；

（2）、过点E作EF∥AB，

∵AB∥CD，

∴AB∥CD∥EF，

∴∠ABE=∠BEF，∠CDE=∠DEF，

∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70°，

∴∠ABE=∠ABC=n°，∠CDE=∠ADC=35°，

∴∠BED=∠BEF+∠DEF=n°+35°；

（3）、过点E作EF∥AB

∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70°

∴∠ABE=∠ABC=n°，∠CDE=∠ADC=35°

∵AB∥CD，

∴AB∥CD∥EF，

∴∠BEF=180°-∠ABE=180°-n°，∠CDE=∠DEF=35°，

∴∠BED=∠BEF+∠DEF=180°-n°+35°=215°-n°.