【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

参考答案:
【答案】![]() ;
;![]() 点
点![]() 或
或![]() ;
;![]() 点P的坐标为
点P的坐标为![]() 或
或![]() .
.
【解析】
(1)由B、C坐标,根据待定系数法可求得直线AB的解析式;(2)由(1)列出AB的方程,求出B的坐标,求出![]() 的面积和
的面积和![]() 的面积,设P的纵坐标为m,代值求出m,再列出直线OC的解析式为
的面积,设P的纵坐标为m,代值求出m,再列出直线OC的解析式为![]() ,当点P在OC上时,求出P点坐标,当点P在BC上时, 求出P点坐标即可;(3)根据直角三角形的性质和点坐标列出解析式解出即可.
,当点P在OC上时,求出P点坐标,当点P在BC上时, 求出P点坐标即可;(3)根据直角三角形的性质和点坐标列出解析式解出即可.
![]() 点A的坐标为
点A的坐标为![]() ,
,
![]() 设直线AB的解析式为
设直线AB的解析式为![]() ,
,
![]() 点
点![]() 在直线AB上,
在直线AB上,
![]() ,
,
![]() ,
,
![]() 直线AB的解析式为
直线AB的解析式为![]() ;
;
![]() 由
由![]() 知,直线AB的解析式为
知,直线AB的解析式为![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ,
,
![]() ,
,
设P的纵坐标为m,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线OC的解析式为
直线OC的解析式为![]() ,
,
当点P在OC上时,![]() ,
,
![]() ,
,
当点P在BC上时,![]() ,
,
![]() ,
,
即:点![]() 或
或![]() ;
;
![]() 是直角三角形,
是直角三角形,
![]() ,
,
当点P在OC上时,由![]() 知,直线OC的解析式为
知,直线OC的解析式为![]() ,
,
![]() 直线BP的解析式的比例系数为
直线BP的解析式的比例系数为![]() ,
,
![]() ,
,
![]() 直线BP的解析式为
直线BP的解析式为![]() ,
,
联立![]() ,解得
,解得 ,
,
![]() ,
,
当点P在BC上时,由![]() 知,直线AB的解析式为
知,直线AB的解析式为![]() ,
,
![]() 直线OP的解析式为
直线OP的解析式为![]() ,联立
,联立![]() 解得,
解得,![]() ,
,
![]() ,
,
即:点P的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,M、N分别为AD、BC的中点,E、F分别是BM、CM的中点.
⑴求证:△ABM≌△DCM;
⑵四边形MENF是什么图形?请证明你的结论;
⑶若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?并请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
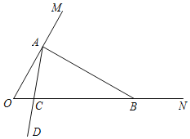
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为 °,△AOB (填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )

A.(35 +55)m
+55)m
B.(25 +45)m
+45)m
C.(25 +75)m
+75)m
D.(50+20 )m
)m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.
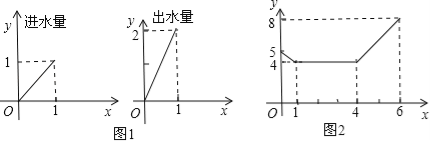
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
相关试题

