【题目】已知x2=1,求![]() 的值.
的值.
解:因为![]() ,所以
,所以![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() 无意义
无意义
所以![]() 的值是1
的值是1
(1)错因:_________________________________.
(2)纠错: _________________________________.
参考答案:
【答案】错在认为负数没有立方根,漏掉了当x=-1时,![]() =-1, 因为x2=1,所以x=±1.当x=1时,
=-1, 因为x2=1,所以x=±1.当x=1时,![]() =
=![]() =1;当x=-1时,
=1;当x=-1时,![]() =
=![]() =-1,所以
=-1,所以![]() 的值是1或-1.
的值是1或-1.
【解析】
如果一个数x的立方等于a,那么x是a的立方根,根据此定义求解即可.
解:(1) 此题错在认为负数没有立方根,漏掉了当x=-1时,![]() =-1;
=-1;
(2) 因为x2=1,所以x=±1.
当x=1时,![]() =
=![]() =1;
=1;
当x=-1时,![]() =
=![]() =-1,
=-1,
所以![]() 的值是1或-1.
的值是1或-1.
故答案为: (1). 错在认为负数没有立方根,漏掉了当x=-1时,![]() =-1, (2). 因为x2=1,所以x=±1.当x=1时,
=-1, (2). 因为x2=1,所以x=±1.当x=1时,![]() =
=![]() =1;当x=-1时,
=1;当x=-1时,![]() =
=![]() =-1,所以
=-1,所以![]() 的值是1或-1.
的值是1或-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠BAC =
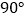 ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)用“*”表示一种新运算:对于任意正实数a,b,都有
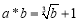 .例如,
.例如,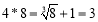 ,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,直线a与直线b交于点O,△ABC的顶点均在格点上.
(1)△ABC向右平移 个单位长度到△A1B1C1位置;
(2)对△ABC分别作下列变换:
① 画出△ABC关于直线a对称的△A2B2C2;
② 将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △ 与△ 成轴对称,对称轴是直线 ;
② △ 与△ 成中心对称,并在图中标出对称中心D的位置.

-
科目: 来源: 题型:
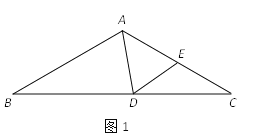
查看答案和解析>>【题目】在△ABC中,∠ABC=∠ACB,点D在BC边所在的直线上,点E在射线AC上,且始终保持∠ADE=∠AED.
(1)如图1,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数;
(2)如图2,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数;
(3)如图3,当点D在BC边的延长线上时,猜想∠BAD与∠CDE的数量关系,并说明理由.
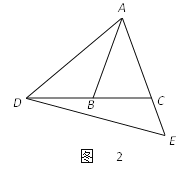
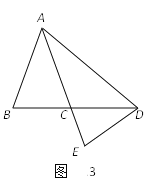
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
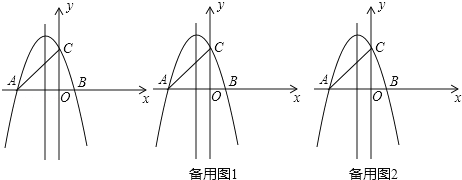
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,直线l与直线AB、CD相交于点E、F,P是射线EA上的一个动点(不包括端点E),将△EFP沿PF折叠,便顶点E落在点Q处.若∠PEF=54°,且∠CFQ=
 ∠CFP,则∠PFE的度数是_____.
∠CFP,则∠PFE的度数是_____.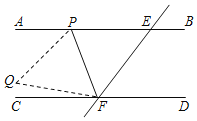
相关试题

