【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
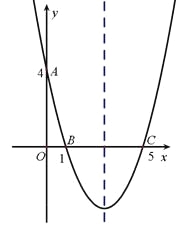
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() ,抛物线的对称轴是 x=3;
,抛物线的对称轴是 x=3;
(2)存在;P点坐标为(3,![]() ).
).
(3)在直线AC下方的抛物线上存在点N,使△NAC面积最大.N(![]() ,-3)
,-3)
【解析】
(1)根据已知条件可设抛物线的解析式为y=a(x-1)(x-5).
把点A(0,4)代入上式,解得a=![]() .
.
∴y=![]() (x-1)(x-5)=
(x-1)(x-5)=![]() x2-
x2-![]() x+4=
x+4=![]() (x-3)2-
(x-3)2-![]() .
.
∴抛物线的对称轴是x=3.
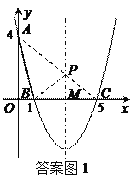
(2)存在,P点的坐标是(3,![]() ).如图1,连接AC交对称轴于点P,连接BP,AB.
).如图1,连接AC交对称轴于点P,连接BP,AB.
∵点B与点C关于对称轴对称,
∴PB=PC.
∴AB+AP+PB=AB+AP+PC=AB+AC.
∴此时△PAB的周长最小.
设直线AC的解析式为y=kx+b.把A(0,4),C(5,0)代入y=kx+b,得
![]() 解得
解得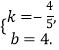
∴y=-![]() x+4.
x+4.
∵点P的横坐标为3,
∴y=-![]() ×3+4=
×3+4=![]() .
.
∴P(3,![]() ).
).
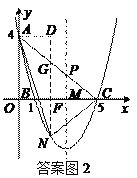
(3)在直线AC下方的抛物线上存在点N,使△NAC的面积最大.
如图2,设N点的横坐标为tt,此时点N(t,![]() t2-
t2-![]() t+4)(0<t<5).
t+4)(0<t<5).
过点N作y轴的平行线,分别交x轴,AC于点F,G,过点A作AD⊥NG,垂足为D.
由(2)可知直线AC的解析式为y=-![]() x+4.
x+4.
把x=t代入y=-![]() x+4,得y=-
x+4,得y=-![]() t+4.
t+4.
∴G(t,-![]() t+4).
t+4).
∴NG=-![]() t+4-(
t+4-(![]() t2-
t2-![]() t+4)=-
t+4)=-![]() t2+4t.
t2+4t.
∵AD+CF=OC=5,
∴S△NAC=S△ANG+S△CGN=![]() NG·AD+
NG·AD+![]() NG·CF=
NG·CF=![]() NG·OC
NG·OC
=![]() ×(-
×(-![]() t2+4t)×5=-2t2+10t=-2(t-
t2+4t)×5=-2t2+10t=-2(t-![]() )2+
)2+![]() .
.
∵当t=![]() 时,△NAC面积的最大值为
时,△NAC面积的最大值为![]() .
.
由t=![]() ,得y=
,得y=![]() ×(
×(![]() )2-
)2-![]() ×
×![]() +4=-3.
+4=-3.
∴N(![]() ,-3).
,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
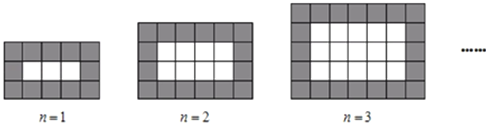
(1)在第4个图中,共有白色瓷砖______块;在第
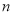 个图中,共有白色瓷砖_____块;
个图中,共有白色瓷砖_____块;(2)试用含
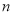 的代数式表示在第
的代数式表示在第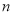 个图中共有瓷砖的块数;
个图中共有瓷砖的块数;(3)如果每块黑瓷砖35元,每块白瓷砖50元,当
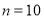 时,求铺设长方形地面共需花多少钱购买瓷砖?
时,求铺设长方形地面共需花多少钱购买瓷砖? -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
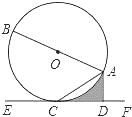
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:如图1,⊙O的半径为2, BC是⊙O的弦,点A是⊙O上的一动点。
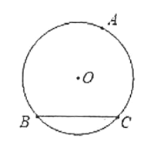
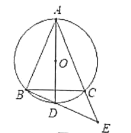
图1 图2
(1)当△ABC的面积最大时,请用尺规作图确定点A位置(尺规作图只保留作图痕迹, 不需要写作法);
(2)如图2,在满足(1)条件下,连接AO并延长交⊙O于点D,连接BD并延长交AC 的延长线于点E,若∠BAC=45° ,求AC2+CE2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列分式方程解应用题:今年植树节,某校师生到距学校20千米的公路旁植树,一班师生骑自行车先走,走了16千米后,二班师生乘汽车出发,结果同时到达.已知汽车的速度比自行车的速度每小时快60千米,求两种车的速度各是多少?
相关试题

