【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
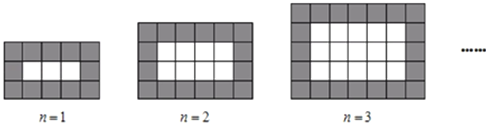
(1)在第4个图中,共有白色瓷砖______块;在第![]() 个图中,共有白色瓷砖_____块;
个图中,共有白色瓷砖_____块;
(2)试用含![]() 的代数式表示在第
的代数式表示在第![]() 个图中共有瓷砖的块数;
个图中共有瓷砖的块数;
(3)如果每块黑瓷砖35元,每块白瓷砖50元,当![]() 时,求铺设长方形地面共需花多少钱购买瓷砖?
时,求铺设长方形地面共需花多少钱购买瓷砖?
参考答案:
【答案】(1)24,![]() ;(2)
;(2)![]() 块;(3)7680元.
块;(3)7680元.
【解析】
(1)通过观察发现规律,第4个图中共有白色瓷砖![]() 块,共有
块,共有![]() 块瓷砖;(2)将上面的规律写出来即可;(3)求出当
块瓷砖;(2)将上面的规律写出来即可;(3)求出当![]() 时黑色和白色瓷砖的个数,然后计算总费用即可.
时黑色和白色瓷砖的个数,然后计算总费用即可.
观察图形发现:
第1个图形中有白色瓷砖![]() 块,共有瓷砖
块,共有瓷砖![]() 块;
块;
第2个图形中有白色瓷砖![]() 块,共有瓷砖
块,共有瓷砖![]() 块;
块;
第3个图形中有白色瓷砖![]() 块,共有瓷砖
块,共有瓷砖![]() 块;
块;
(1)第4个图形中有白色瓷砖![]() 块,第
块,第![]() 个图形中有白色瓷砖
个图形中有白色瓷砖![]() 块;
块;
故答案为24,![]() ;
;
(2)共有瓷砖![]() 块;
块;
(3)当![]() 时,共有白色瓷砖120块,黑色瓷砖48块,
时,共有白色瓷砖120块,黑色瓷砖48块,
![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx+c的图象过点(4,3)、(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在下图中作出此二次函数的图象,根据图象说明,当x取何值时,y<0?

-
科目: 来源: 题型:
查看答案和解析>>【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量
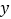 (件)是销售单价
(件)是销售单价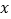 (元/件)的一次函数.
(元/件)的一次函数.销售单价
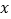 (元/件)
(元/件)…
30
40
50
60
…
每天销售量
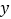 (件)
(件)…
350
300
250
200
…
(1)求出
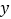 与
与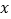 的函数关系;
的函数关系;(2)物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪:
①当销售单价
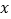 取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);②试确定销售单价
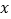 取何值时,花店销该鲜花礼盒每天获得的利润
取何值时,花店销该鲜花礼盒每天获得的利润 (元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
(元)最大?并求出花店销该鲜花礼盒每天获得的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
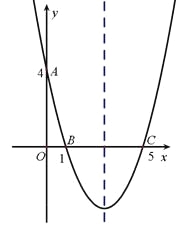
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
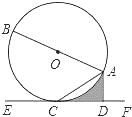
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
相关试题

