【题目】己知:如图1,⊙O的半径为2, BC是⊙O的弦,点A是⊙O上的一动点。
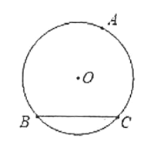
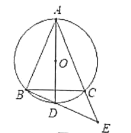
图1 图2
(1)当△ABC的面积最大时,请用尺规作图确定点A位置(尺规作图只保留作图痕迹, 不需要写作法);
(2)如图2,在满足(1)条件下,连接AO并延长交⊙O于点D,连接BD并延长交AC 的延长线于点E,若∠BAC=45° ,求AC2+CE2的值.
参考答案:
【答案】(1)见解析;(2)16.
【解析】
(1)作BC的垂直平分线交优弧BC于A,则点A满足条件;
(2)利用圆周角定理得到∠ACD=90°,根据圆内接四边形的性质得∠CDE=∠BAC=45°,通过判断△DCE为等腰直角三角形得到CE=CD,然后根据勾股定理得到AC2+CE2=AC2+CD2=AD2.
解:(1)如图1,点A为所作;
(2)如图2,连接CD,
∵AD为直径,
∴∠ACD=90°,
∵∠CDE=∠BAC=45°,
∴△DCE为等腰直角三角形,
∴CE=CD,
∴AC2+CE2=AC2+CD2=AD2=42=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
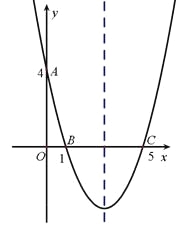
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
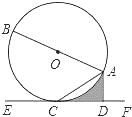
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列分式方程解应用题:今年植树节,某校师生到距学校20千米的公路旁植树,一班师生骑自行车先走,走了16千米后,二班师生乘汽车出发,结果同时到达.已知汽车的速度比自行车的速度每小时快60千米,求两种车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=x的图象与函数y=
 (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m).(1)求m,k的值;
(2)直线y=4与函数y=x的图象相交于点A,与函数y=
 (x>0)的图象相交于点B,求线段AB长.
(x>0)的图象相交于点B,求线段AB长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量
单价
不超过
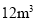 的部分
的部分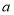 元/
元/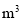
超过
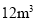 但不超过
但不超过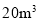 的部分
的部分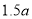 元/
元/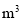
超过
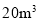 的部分
的部分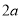 元/
元/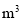
(1)当
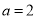 时,某用户一个月用了
时,某用户一个月用了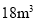 水,求该用户这个月应缴纳的水费;
水,求该用户这个月应缴纳的水费;(2)设某户月用水量为
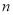 立方米,当
立方米,当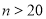 时,求该用户应缴纳的水费(用含
时,求该用户应缴纳的水费(用含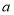 、
、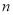 的整式表示);
的整式表示);(3)当
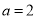 时,甲、乙两用户一个月共用水
时,甲、乙两用户一个月共用水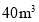 .已知甲用户用水量超过了
.已知甲用户用水量超过了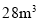 ,设甲用户这个月用水如
,设甲用户这个月用水如,试求甲、乙两用户一个月共缴纳的水费.(用含
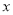 的整式表示)
的整式表示)
相关试题

