【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

参考答案:
【答案】4
【解析】
由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,
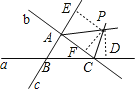
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故答案是:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面
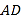 与通道
与通道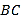 平行),通道水平宽度
平行),通道水平宽度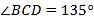 为8米,
为8米,  ,通道斜面
,通道斜面 的长为6米,通道斜面
的长为6米,通道斜面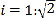 的坡度
的坡度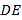 .
.(1)求通道斜面
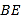 的长为 米;
的长为 米;(2)为增加市民行走的舒适度,拟将设计图中的通道斜面
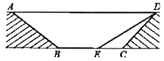 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面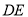 的坡角为30°,求此时
的坡角为30°,求此时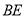 的长.(结果保留根号)
的长.(结果保留根号)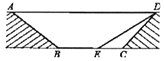
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 交y轴于点A,交直线x=6于点B.
交y轴于点A,交直线x=6于点B.(1)填空:抛物线的对称轴为x=_________,点B的纵坐标为__________(用含a的代数式表示);
(2)若直线AB与x轴正方向所夹的角为45°时,抛物线在x轴上方,求
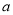 的值;
的值;(3)记抛物线在A、B之间的部分为图像G(包含A、B两点),若对于图像G上任意一点
 ,总有
,总有 ≤3,求a的取值范围.
≤3,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
如图,∠1=∠2,∠A=∠D, 求证:∠B=∠C.
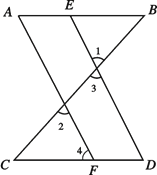
证明:∵∠1=∠2(已知),
∠1=∠3( ),
∴∠2=∠3(等量代换).
∴AF∥________( ).
∴∠D=∠4(两直线平行,同位角相等 ).
∵∠A=∠D(已知),
∴∠A=∠4(等量代换).
∴AB∥CD(内错角相等,两直线平行).
∴∠B=∠C( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选
取该校100名学生进行调查,要求每名学生只选出一类自己最喜爱的节目,根据调查结果 绘制了不完整的条形图和扇形统计图(如图),
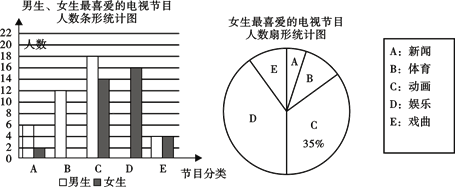
根据图中提供的信息,解答下列问题:
(1)这次抽样调查的女生人数是_______人;
(2)扇形统计图中, “A”组对应的圆心角度数为_______,并将条形图中补充完整;
(3)若该校有 1800 名学生,试估计全校最喜欢新闻和戏曲的学生一共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长青农产品加工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批原料甲运回工厂,经过加工后制成产品乙运到 B 地,其中原料甲和产品乙的重量都是正整数.
已知铁路运价为 2 元/(吨·千米),公路运价为 8 元/(吨·千米).

(1)若由 A 到 B 的两次运输中,原料甲比产品乙多 9 吨,工厂计划支出铁路运费超 过 5700 元,公路运费不超过 9680 元.问购买原料甲有哪几种方案,分别是多少吨?
(2)由于国家出台惠农政策,对运输农产品的车辆免收高速通行费,并给予一定的 财政补贴,综合惠农政策后公路运输价格下降 m( 0 m 4 且 m 为整数)元, 若由 A 到 B 的两次运输中,铁路运费为 5760 元,公路运费为 5100 元,求 m 的 值.
相关试题

