【题目】在平面直角坐标系xOy中,抛物线![]() 交y轴于点A,交直线x=6于点B.
交y轴于点A,交直线x=6于点B.
(1)填空:抛物线的对称轴为x=_________,点B的纵坐标为__________(用含a的代数式表示);
(2)若直线AB与x轴正方向所夹的角为45°时,抛物线在x轴上方,求![]() 的值;
的值;
(3)记抛物线在A、B之间的部分为图像G(包含A、B两点),若对于图像G上任意一点![]() ,总有
,总有![]() ≤3,求a的取值范围.
≤3,求a的取值范围.

参考答案:
【答案】 (1)![]() ;
; ![]() ;(2)a=
;(2)a=![]() ;(3)a≥
;(3)a≥![]() 或a<0.
或a<0.
【解析】(1). ![]() ;
;![]() ; (2)
; (2)![]() ; (3)
; (3) ![]() 或a<0.
或a<0.
试题分析:(1)①根据抛物线的对称轴为直线![]() ,代入数据即可得出结论;②把x=6代入直线
,代入数据即可得出结论;②把x=6代入直线![]() 即可求出点B的纵坐标;
即可求出点B的纵坐标;
(2)根据直线AB与x轴正方向所夹的角为45°,列方程-30a2+36a+3=6+3求出a的值;
(3)分a>0及a<0两种情况考虑,依照题意画出函数图象,利用数形结合即可得出a的取值范围.
解:(1)①对称轴为: ![]() ;
;
②把x=6代入直线![]() 得,
得,
y=36a-30a2+3.
∴点B的纵坐标为-30a2+36a+3.
(2)当x=0时, ![]() =3,
=3,
∴A(0,3).
∵直线AB与x轴正方向所夹的角为45°,
∴-30a2+36a+3=6+3,
解之得
![]() ,a2=1(舍去).
,a2=1(舍去).
∴a的值是![]() .
.
(3)当a>0时,如图1.
∵A(0,3),
∴要使0≤xp≤6时,始终满足yp≤3,只需使抛物线y=ax2-5a2x+3的对称轴与直线x=3重合或在直线x=3的右侧.
∴![]() ,
,
![]() .
.
当a<0时,如图2,
在0≤xp≤6中,yp≤3恒成立.
综上所述,a的取值范围为![]() 或a<0.
或a<0.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图①是一个四边形纸条 ABCD,其中 AB∥CD,E,F 分别为边 AB,CD 上的两个点,将纸条 ABCD 沿 EF 折叠得到图②,再将图②沿 DF 折叠得到图③,若在图③中,∠FEM=26°,则∠EFC 的度数为( )

A.52°B.64°C.102°D.128°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面
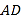 与通道
与通道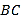 平行),通道水平宽度
平行),通道水平宽度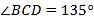 为8米,
为8米,  ,通道斜面
,通道斜面 的长为6米,通道斜面
的长为6米,通道斜面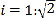 的坡度
的坡度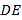 .
.(1)求通道斜面
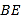 的长为 米;
的长为 米;(2)为增加市民行走的舒适度,拟将设计图中的通道斜面
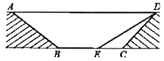 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面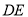 的坡角为30°,求此时
的坡角为30°,求此时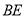 的长.(结果保留根号)
的长.(结果保留根号)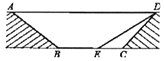
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
如图,∠1=∠2,∠A=∠D, 求证:∠B=∠C.
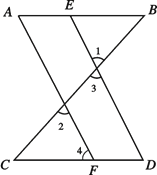
证明:∵∠1=∠2(已知),
∠1=∠3( ),
∴∠2=∠3(等量代换).
∴AF∥________( ).
∴∠D=∠4(两直线平行,同位角相等 ).
∵∠A=∠D(已知),
∴∠A=∠4(等量代换).
∴AB∥CD(内错角相等,两直线平行).
∴∠B=∠C( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选
取该校100名学生进行调查,要求每名学生只选出一类自己最喜爱的节目,根据调查结果 绘制了不完整的条形图和扇形统计图(如图),
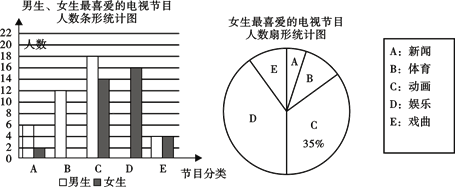
根据图中提供的信息,解答下列问题:
(1)这次抽样调查的女生人数是_______人;
(2)扇形统计图中, “A”组对应的圆心角度数为_______,并将条形图中补充完整;
(3)若该校有 1800 名学生,试估计全校最喜欢新闻和戏曲的学生一共有多少人?
相关试题

