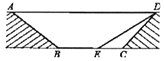
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
参考答案:
【答案】(1)7.4米;(2)(8+3![]() -3
-3![]() )米
)米
【解析】试题分析: (1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,根据已知得出DM=CM=![]() CD=3
CD=3![]() ,则AN=DM=3
,则AN=DM=3![]() ,再解Rt△ANB,由通道斜面AB的坡度i=1:
,再解Rt△ANB,由通道斜面AB的坡度i=1: ![]() ,得出BN=
,得出BN=![]() AN=6,然后根据勾股定理求出AB;
AN=6,然后根据勾股定理求出AB;
(2)先解Rt△MED,求出EM=![]() DM=3
DM=3![]() ,得出EC=EM-CM=3
,得出EC=EM-CM=3![]() -3
-3![]() ,再根据BE=BC-EC即可求解.
,再根据BE=BC-EC即可求解.
试题解析:(1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,
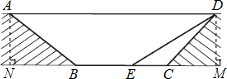
∵∠BCD=135°,
∴∠DCM=45°.
∵在Rt△CMD中,∠CMD=90°,CD=6,
∴DM=CM=![]() CD=3
CD=3![]() ,
,
∴AN=DM=3![]() ,
,
∵通道斜面AB的坡度i=1: ![]() ,
,
∴tan∠ABN=![]() ,
,
∴BN=![]() AN=6,
AN=6,
∴AB=![]() =3
=3![]() ≈7.4.
≈7.4.
即通道斜面AB的长约为7.4米;
(2)∵在Rt△MED中,∠EMD=90°,∠DEM=30°,DM=3![]() ,
,
∴EM=![]() DM=3
DM=3![]() ,
,
∴EC=EM-CM=3![]() -3
-3![]() ,
,
∴BE=BC-EC=8-(3![]() -3
-3![]() )=(8+3
)=(8+3![]() -3
-3![]() )米
)米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 E 在 AD 的延长线上,下列条件中能判断 AB∥CD 的是( )

A. ∠1=∠4B. ∠2=∠3C. ∠C=∠CDED. ∠C+∠CDA=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图①是一个四边形纸条 ABCD,其中 AB∥CD,E,F 分别为边 AB,CD 上的两个点,将纸条 ABCD 沿 EF 折叠得到图②,再将图②沿 DF 折叠得到图③,若在图③中,∠FEM=26°,则∠EFC 的度数为( )

A.52°B.64°C.102°D.128°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 交y轴于点A,交直线x=6于点B.
交y轴于点A,交直线x=6于点B.(1)填空:抛物线的对称轴为x=_________,点B的纵坐标为__________(用含a的代数式表示);
(2)若直线AB与x轴正方向所夹的角为45°时,抛物线在x轴上方,求
 的值;
的值;(3)记抛物线在A、B之间的部分为图像G(包含A、B两点),若对于图像G上任意一点
 ,总有
,总有 ≤3,求a的取值范围.
≤3,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
如图,∠1=∠2,∠A=∠D, 求证:∠B=∠C.
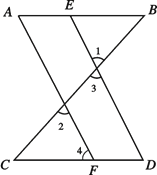
证明:∵∠1=∠2(已知),
∠1=∠3( ),
∴∠2=∠3(等量代换).
∴AF∥________( ).
∴∠D=∠4(两直线平行,同位角相等 ).
∵∠A=∠D(已知),
∴∠A=∠4(等量代换).
∴AB∥CD(内错角相等,两直线平行).
∴∠B=∠C( ).
相关试题

