【题目】在△ABC中AB=AC,∠BAC=90°,分别过B、C作过A点的直线的垂线,垂足为D、E.
(1)求证:△AEC≌△BDA;
(2)如果CE=2,BD=4,求ED的长是多少?

参考答案:
【答案】(1)证明见解析;(2)6.
【解析】
(1)由题意得出∠CEA=90°,∠ADB=90°,证得∠ACE=∠BAD,由AAS即可证得△AEC≌△BDA;
(2)由△AEC≌△BDA,得出AD=CE=2,AE=BD=4,即可得出结果.
(1)∵CE⊥ED,
∴∠CEA=90°,
∵BD⊥ED,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠CAE+∠BAD=90°,
∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAD,
在△AEC和△BDA中,
 ,
,
∴△AEC≌△BDA(AAS);
(2)∵△AEC≌△BDA,
∴AD=CE=2,AE=BD=4,
∴ED=AE+AD=4+2=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(
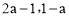 )在第一象限,则a的取值范围在数轴上表示正确的是
)在第一象限,则a的取值范围在数轴上表示正确的是A.
 B.
B.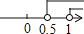 C.
C. D.
D.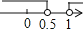
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+
x2+  x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示:
(1)比a与b的和小3的数.
(2)比a与b的差的一半大1的数.
(3)比a除以b的商的3倍大8的数.
(4)比a除b的商的3倍大8的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣  x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.

(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.
相关试题

