【题目】已知点A(-3,0),B(1,0).
(1)在y轴上找一点C,使之满足S△ABC=6,求点C的坐标;
(2)在y轴上找一点D,使AD=AB,求点D的坐标.
参考答案:
【答案】(1)点C的坐标为(0,3)或(0,-3);(2) D(0,![]() )或(0,-
)或(0,-![]() ).
).
【解析】
(1)由A(-3,0),B(1,0),可得AB=4,再由S△ABC=6,可得△ABC边AB上的高为3,即可得到点C的纵坐标![]() ,由此即可求得点C的坐标;(2)由题意可知AD=AB=4,AO=3,∠AOD=90°根据勾股定理求得OD=
,由此即可求得点C的坐标;(2)由题意可知AD=AB=4,AO=3,∠AOD=90°根据勾股定理求得OD=![]() ,由此即可求得点D的坐标.
,由此即可求得点D的坐标.
(1) ∵A(-3,0),B(1,0).
∴AB=4,
∵S△ABC=6,
∴△ABC边AB上的高为3,即点C的纵坐标![]() ,
,
∴点C的坐标为(0,3)或(0,-3).
(2)∵A(-3,0),B(1,0),∴AB=4,AO=3.
又∠AOD=90°,
∴OD=![]() =
=![]() ,
,
∴D(0,![]() )或(0,-
)或(0,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出点A′,B′,C′的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个n位自然数
 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数 能被(x0+1)整除,再依次轮换个位数字得到的新数
能被(x0+1)整除,再依次轮换个位数字得到的新数 能被(x0+2)整除,按此规律轮换后,
能被(x0+2)整除,按此规律轮换后, 能被(x0+3)整除,…,
能被(x0+3)整除,…, 能被(x0+n﹣1)整除,则称这个n位数
能被(x0+n﹣1)整除,则称这个n位数 是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”.再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”.再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.(1)请判断:自然数24 “轮换数”,245 “轮换数”(填“是”或“不是”);
(2)若一个两位自然数的个位数字是m(0<m<5,且为整数),十位数字是2m,试说明:这个两位自然数一定是“轮换数”;
(3)若三位自然数
 是4的一个“轮换数”,其中b=0,请直接写出这个三位自然数
是4的一个“轮换数”,其中b=0,请直接写出这个三位自然数 .
. -
科目: 来源: 题型:
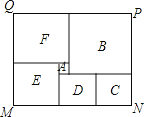
查看答案和解析>>【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠BOC=α.
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=
 ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)若∠AOD=
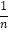 ∠AOC,∠DOE=
∠AOC,∠DOE=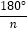 (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).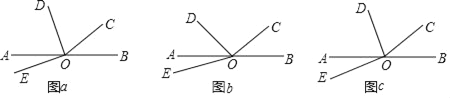
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两点在数轴上的位置如图所示,其中O为原点,点A对应的有理数为﹣4,点B对应的有理数为6.
(1)动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0).
①当t=1时,AP的长为 ,点P表示的有理数为 ;
②当PB=2时,求t的值;
(2)如果动点P以每秒6个单位长度的速度从O点向右运动,点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,且三点同时出发,那么经过几秒PA=2PB.

相关试题

