【题目】A,B两点在数轴上的位置如图所示,其中O为原点,点A对应的有理数为﹣4,点B对应的有理数为6.
(1)动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0).
①当t=1时,AP的长为 ,点P表示的有理数为 ;
②当PB=2时,求t的值;
(2)如果动点P以每秒6个单位长度的速度从O点向右运动,点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,且三点同时出发,那么经过几秒PA=2PB.
![]()
参考答案:
【答案】(1)①2,﹣2 ②t=6 (2) ①t=![]() 秒或16秒时, PA=2PB
秒或16秒时, PA=2PB
【解析】分析:(1)①根据路程=速度×时间,以及线段的和差定义计算即可;
②分两种情形分别求解即可;
(2)分两种情形:P在A、B之间或者P在B点右侧的情况,分别构建方程即可解决问题;
详解:(1)①∵动点P从点A出发,以每秒2个单位长度的速度向右运动,
∴当t=1时,AP=2,
∵OA=4,
∴OP=2,
∴点P表示的有理数为﹣2.
②当点P在B左侧时,∵AB=10,PB=2,
∴AP=8,
∴t=4.
当点P在点B右侧时,AP=12,
∴t=6;
(2)设一点时间为t秒;
①当P在A、B之间时,PA=4+6t=4+5t,PB=6+3t﹣6t=6﹣3t,
∵PA=2PB,
∴4+5t=2(6﹣3t),
解得t=![]() .
.
②当P点在B点右侧时,PA=4+5t,PB=3t﹣6,
∵PA=2PB,
∴4+5t=2(3t﹣6),
解得t=16,
故经过![]() 秒或16秒时,PA=2PB.
秒或16秒时,PA=2PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-3,0),B(1,0).
(1)在y轴上找一点C,使之满足S△ABC=6,求点C的坐标;
(2)在y轴上找一点D,使AD=AB,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠BOC=α.
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=
 ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)若∠AOD=
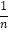 ∠AOC,∠DOE=
∠AOC,∠DOE=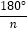 (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).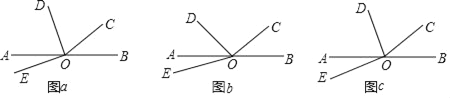
-
科目: 来源: 题型:
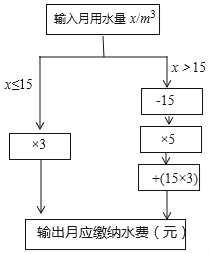
查看答案和解析>>【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户
张大爷
王阿姨
小明家
月用水量/m3
6
15
17
月应缴纳水费/元
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1、x2
(1)求实数k的取值范围;
(2)若x1、x2满足|x1|+|x2|=|x1x2|﹣1,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )

A. 13 cm B. 14 cm C. 15 cm D. 16 cm
相关试题

