【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被(x0+1)整除,再依次轮换个位数字得到的新数
能被(x0+1)整除,再依次轮换个位数字得到的新数![]() 能被(x0+2)整除,按此规律轮换后,
能被(x0+2)整除,按此规律轮换后,![]() 能被(x0+3)整除,…,
能被(x0+3)整除,…,![]() 能被(x0+n﹣1)整除,则称这个n位数
能被(x0+n﹣1)整除,则称这个n位数![]() 是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”.再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”.再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)请判断:自然数24 “轮换数”,245 “轮换数”(填“是”或“不是”);
(2)若一个两位自然数的个位数字是m(0<m<5,且为整数),十位数字是2m,试说明:这个两位自然数一定是“轮换数”;
(3)若三位自然数![]() 是4的一个“轮换数”,其中b=0,请直接写出这个三位自然数
是4的一个“轮换数”,其中b=0,请直接写出这个三位自然数![]() .
.
参考答案:
【答案】(1)是,不是;(2)详见解析;(3)504.
【解析】
(1)分别判断能否被两个联系的整数整除即可;
(2)表示出这个两位自然数,和轮换两位自然数,得到能整除即可;
(3)先表示出三位自然数和轮换三位自然数,再根据能被5整除,得出b的可能值,进而用4整除,得出c的可能值,最后用能被3整除即可.
(1)∵24是6的倍数,42是7的倍数,
∴自然数24是“轮换数”;
∵245的约数是5、7、7,452的约数有2、2、113;
当245被5整除时,而452不能被6整除;
当245被7整除时,而452不能被8整除;
∴245不是“轮换数”.
(2)此两位数为20m+m=21m=7m×3,是3的倍数; 轮换后为10m+2m=12m=4m×4,是4的倍数;
∴这个两位自然数一定是“轮换数”.
(3)此三位数为:100a+10b+c
当b=0时,三位数为:100a+10b+c=100a+c,
∵100a+c是4的倍数,而100a是4的倍数,
∴c是4的倍数,
∴c=4或8;
若c=4,轮换后为40+a是5的倍数,
∴a=5;
验证:再次轮换后为450是6的倍数,即这个三位数为:504
若c=8,则三位数为:100a+8;
轮换后为80+a是5的倍数,
∴a=5;
验证:再次轮换后为850不是6的倍数,即c=8舍去
综上所述,这个三位数为:504.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲,乙两个区内进行了调查统计,将调查结果分为很满意,满意,不满意,很不满意四类,回收、整理好全部问卷后,得到下列不完整的统计图. 请结合图中信息,解决下列问题:

(1)参加这次调查的总人数为人,其中调查结果为“满意”的人数是人,调查结果为“很不满意”的人数占总人数的百分比为 , 扇形图中“不满意”部分对应扇形的圆心角为度.
(2)兴趣小组准备从调查结果为“很不满意”的4位市民中随机选择2位进行回访,已知这4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
(1)a+b= ,
 = ;
= ;(2)判断b+c,a﹣c,(b+c)(a﹣b)的符号;
(3)判断
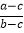 的符号.
的符号.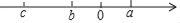
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出点A′,B′,C′的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
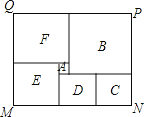
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-3,0),B(1,0).
(1)在y轴上找一点C,使之满足S△ABC=6,求点C的坐标;
(2)在y轴上找一点D,使AD=AB,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

相关试题

