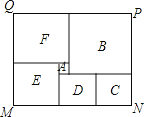
【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
参考答案:
【答案】143.
【解析】
试题分析:由题可知,由于矩形平面示意图中全是正方形,则右下角两个小正方形一样大小,而顺时针方向每个大正方形边长都增大1,等量关系:边长都是旁边一个正方形边长+最小正方形边长.
解:设右下方两个并排的正方形的边长为x,
则x+2+x+3=x+1+x+x,
解得x=4
所以长方形长为3x+1=13,
宽为2x+3=11,
所以长方形面积为13×11=143.
答:结果为143.
故答案为:143.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D.
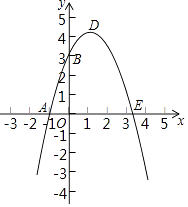
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出P点的坐标,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABCD中,AB=5,AD=8,∠A=60°,点P为AD边上任意一点,连接PB,并将PB绕点P逆时针旋转90°得到线段PB′.
(1)当∠DP B′=20°时,∠ABP=____________;
(2)如图2,连结BB′,点P从A运动到D的过程中,求△PBB′面积的取值范围;
(3)若点B′恰好落在
 ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)
ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)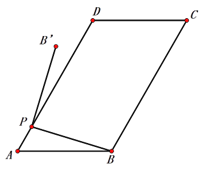
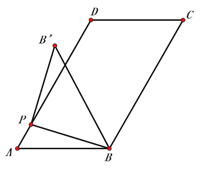
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;
③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( )
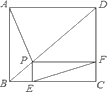
A. ①② B. ①④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c=0;④若点B(﹣
 ,y1)、C(﹣
,y1)、C(﹣  ,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可)
,y2)为函数图象上的两点,则y1<y2 , 其中正确结论是:(填上序号即可) 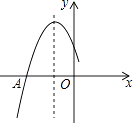
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=
 ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC的边长为4, P、Q、R分别为边AB、BC、AC上的动点,则PR+QR的最小值是 _____.
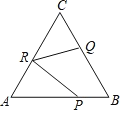
相关试题

