搜索
【题目】已知线段MN=10cm，点C是直线MN上一点，NC=4cm，若P是线段MN的中点，Q是线段NC的中点，则线段PQ的长度是（ ）
A.7cmB.7cm或3cmC.5cmD.3cm
参考答案：
【答案】B
【解析】
分两种情况：点C在线段MN上和点C在线段MN的延长线上，当点C在线段MN上时，利用中点求出PN,QN的长度，然后利用
即可求解；当点C在线段MN的延长线上时，利用中点求出PN,QN的长度，然后利用
即可求解．
若点C在线段MN上，如图，
∵P是线段MN的中点，MN=10cm，
∴
，
∵Q是线段CN的中点，CN=4cm，
∴
，
；
若点C在线段MN的延长线上，如图，
∵P是线段MN的中点，MN=10cm，
∴ ，
∵Q是线段CN的中点，CN=4cm，
∴ ，
；
综上所述，PQ的长度为7cm或3cm．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】西安爱知中学为了全面提高学生的综合素养，学校组织了音乐，篮球，跆拳道，美术共四个社团，初学生积极参加(每个学生限报一项)，参加社团的学生共有
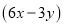人，其中音乐社团有
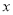人参加，篮球社团参加的人数比音乐社团参加的人数的两倍少
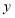人，跆拳道社团参加的人数比篮球社团参加的人数一半多1人（1）篮球社团有 人．(用含
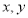的式子表示)（2）求篮球社团比跆拳道社团多多少人？(用含
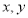的式子表示)（3）若
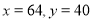，求美术社团的人数 -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：在数轴上表示两个数
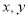的点之间的距离可以表示为
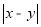，比如表示3的点与-2的点之间的距离表示为
；
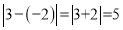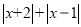可以表示数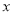
的点与表示数1的点之间的距离与表示数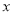的点与表示数-2的点之间的距离的和，根据上述材料，回答下列问题：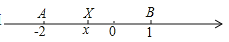
（1）解方程
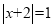
（2）
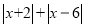的最小值是 ． （3）
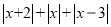的最小值是 此时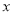的值为 ．拓展推广：如图所示：当表示数
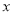的点在点
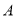和点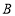
之间(包含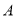点和点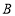)时，表示数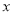的点与点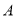的距离与表示数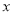的点和点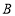的距离之和最小，且最小值为3，即
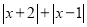的最小值是3，且此时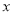的取值范围为 （4）已知数
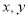满足
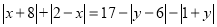则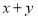
的最小值是 最大值是 ． （5）当
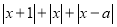的最小值是4.5时，求出
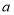的值及对应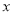的值或取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克）
…
34.8
32
29.6
28
…
售价x（元/千克）
…
22.6
24
25.2
26
…
（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．
（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？
-
科目： 来源： 题型：
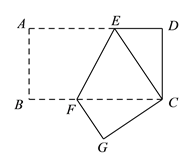
查看答案和解析>>【题目】已知将一矩形纸片ABCD折叠，使顶点A与C重合，折痕为EF．
（1）求证：CE=CF；
（2）若AB =8 cm，BC=16 cm，连接AF，写出求四边形AFCE面积的思路．
-
科目： 来源： 题型：
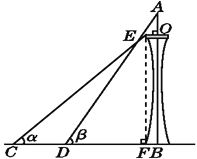
查看答案和解析>>【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
-
科目： 来源： 题型：
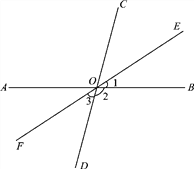
查看答案和解析>>【题目】如图，直线AB、CD相交于点O，∠BOC＝80°，OE是∠BOC的角平分线，OF是OE的反向延长线．
（1）求∠2、∠3的度数；
（2）说明OF平分∠AOD的理由．
相关试题
