【题目】阅读材料:在数轴上表示两个数![]() 的点之间的距离可以表示为
的点之间的距离可以表示为![]() ,比如表示3的点与-2的点之间的距离表示为
,比如表示3的点与-2的点之间的距离表示为![]() ;
;![]() 可以表示数
可以表示数![]() 的点与表示数1的点之间的距离与表示数
的点与表示数1的点之间的距离与表示数![]() 的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
![]()
(1)解方程![]()
(2)![]() 的最小值是 .
的最小值是 .
(3)![]() 的最小值是 此时
的最小值是 此时![]() 的值为 .
的值为 .
拓展推广:如图所示:当表示数![]() 的点在点
的点在点![]() 和点
和点![]() 之间(包含点
之间(包含点![]() 和点
和点![]() )时,表示数
)时,表示数![]() 的点与点
的点与点![]() 的距离与表示数
的距离与表示数![]() 的点和点
的点和点![]() 的距离之和最小,且最小值为3,即
的距离之和最小,且最小值为3,即![]() 的最小值是3,且此时
的最小值是3,且此时![]() 的取值范围为
的取值范围为
(4)已知数![]() 满足
满足![]() 则
则![]()
(5)当![]() 的最小值是4.5时,求出
的最小值是4.5时,求出![]() 的值及对应
的值及对应![]() 的值或取值范围.
的值或取值范围.
参考答案:
【答案】(1)x=-1或x=-3(2)8;(3)5; 0;拓展推广: -2≤x≤1;(4)-9;8;(5)a=3.5,x=0或a=-4.5, x=-1.
【解析】
(1)根据题意及绝对值的含义即可求解;
(2)根据绝对值的几何意义,得出![]() 的最小值;
的最小值;
(3)根据绝对值的几何意义,得出![]() 的最小值及x的值;
的最小值及x的值;
拓展推广:根据绝对值的几何意义,可得![]() 取最小值时,x的取值为-2≤x≤1;
取最小值时,x的取值为-2≤x≤1;
(4)根据![]() 变形得
变形得![]() ,根据题意及绝对值的几何含义得到x,y的取值即可求解;
,根据题意及绝对值的几何含义得到x,y的取值即可求解;
(5)根据题意分a>0和a<-1两种情况分别求解即可.
(1)解![]()
x+2=1或x+2=-1
解得x=-1或x=-3
(2)根据绝对值的几何意义可得,当2≤x≤6时,![]() 的最小值是8
的最小值是8
故答案为:8;
(3)根据绝对值的几何意义可得,当x=0时,![]() 的最小值是5,
的最小值是5,
故答案为:5; 0;
拓展推广:根据绝对值的几何意义可得:当![]() 的最小值是3时,x的取值为-2≤x≤1
的最小值是3时,x的取值为-2≤x≤1
故答案为:-2≤x≤1;
(4)∵![]()
∴![]()
∵![]() 的最小值为10,
的最小值为10,![]() 的最小值为7,
的最小值为7,
根据绝对值的几何含义可得x的取值是-8≤x≤2;y的取值是-1≤x≤6
故当x=-8,y=-1时![]() 的最小值是-9;
的最小值是-9;
故当x=2,y=6时![]() 的最大值是8;
的最大值是8;
故答案为:-9;8;
(5)如图,当a>0时,∵![]() 的最小值是4.5
的最小值是4.5
∴a=4.5-1=3.5,此时x=0
当a<-1时,∵![]() 的最小值是4.5
的最小值是4.5
∴a=0-4.5=-4.5, 此时x=-1.
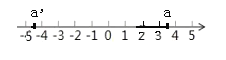
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
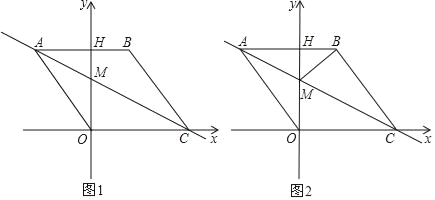
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<
 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在分别标有号码2,3,4…10的9个球中,随机取出2个球,记下它们的号码,则较大号能被较小号整除的概率是( )
A.
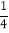 B.
B.  C.
C. 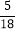 D.
D. 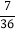
-
科目: 来源: 题型:
查看答案和解析>>【题目】西安爱知中学为了全面提高学生的综合素养,学校组织了音乐,篮球,跆拳道,美术共四个社团,初学生积极参加(每个学生限报一项),参加社团的学生共有
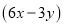 人,其中音乐社团有
人,其中音乐社团有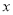 人参加,篮球社团参加的人数比音乐社团参加的人数的两倍少
人参加,篮球社团参加的人数比音乐社团参加的人数的两倍少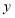 人,跆拳道社团参加的人数比篮球社团参加的人数一半多1人
人,跆拳道社团参加的人数比篮球社团参加的人数一半多1人(1)篮球社团有 人.(用含
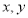 的式子表示)
的式子表示)(2)求篮球社团比跆拳道社团多多少人?(用含
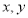 的式子表示)
的式子表示)(3)若
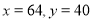 ,求美术社团的人数
,求美术社团的人数 -
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克)
…
34.8
32
29.6
28
…
售价x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
A.7cmB.7cm或3cmC.5cmD.3cm
-
科目: 来源: 题型:
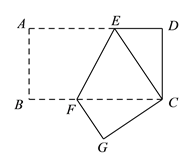
查看答案和解析>>【题目】已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)求证:CE=CF;
(2)若AB =8 cm,BC=16 cm,连接AF,写出求四边形AFCE面积的思路.
相关试题

