【题目】已知二次函数y=4x2﹣4ax+a2﹣2a+2,
(1)当a=0,2,4时,请在同一直角坐标系中画出对应函数图象的顶点,并画出a=2 时的函数图象;
(2)证明当a取任意实数时,顶点在一条确定的直线上;
(3)求(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长.
参考答案:
【答案】
(1)解:∵二次函数y=4x2﹣4ax+a2﹣2a+2=4(x﹣ ![]() a)2﹣2a+2,
a)2﹣2a+2,
∴抛物线的顶点坐标为( ![]() a,﹣2a+2).
a,﹣2a+2).
当a=0时,抛物线的顶点坐标为(0,2);
当a=2时,抛物线的顶点坐标为(1,﹣2),抛物线的解析式为y=4(x﹣1)2﹣2;
当a=4时,抛物线的顶点坐标为(2,﹣6).
画出函数图象如图所示
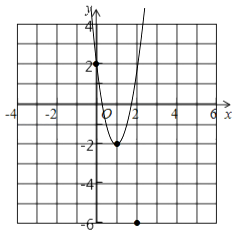
(2)证明:∵抛物线的顶点坐标为( ![]() a,﹣2a+2),
a,﹣2a+2),
∴﹣2a+2=﹣4×( ![]() a)+2,
a)+2,
∴y=﹣4x+2,即当a取任意实数时,顶点在一条确定的直线上
(3)解:联立两函数解析式成方程组,
![]() ,解得:
,解得: 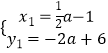 ,
, 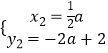 ,
,
∴两函数的交点坐标为( ![]() a﹣1,﹣2a+6),(
a﹣1,﹣2a+6),( ![]() a,﹣2a+2),
a,﹣2a+2),
∴(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长为 ![]() =
= ![]()
【解析】(1) 利用配方法将二次函数解析式由一般式变形为顶点式,由此可得出抛物线的顶点坐标,分别代入a=0、a=2、a=4找出顶点坐标,并画出a=2时,二次函数的图象即可;
(2)由待定系数法,将抛物线的顶点坐标代入直线的解析式,消去a后即可得出y=-4x+2,此题得证;
(3)联立两函数解析式成方程组,通过解方程组求出交点坐标,再根据两点间的距离公式求出线段长度即可.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图1中的BD和CE就是两条三分线.

(1)请你在图2中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(画出一种即可);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,请在图3上画出示意图;
(3)在(2)的前提下,设∠C=x°,试求出x所有可能的值. -
科目: 来源: 题型:
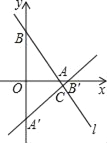
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣2x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
(1)求直线A′B′所对应的函数表达式.
(2)若直线A′B′与直线AB相交于点C,求△A′BC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<
 的解集(请直接写出答案).
的解集(请直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.

(1)求证:△ADE∽△PQD;
(2)求线段CQ的长;
(3)求∠EGB的正切值. -
科目: 来源: 题型:
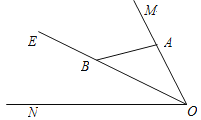
查看答案和解析>>【题目】如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调
彩电
进价(元/台)
5400
3500
售价(元/台)
6100
3900
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
相关试题

