【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图1中的BD和CE就是两条三分线.
(1)请你在图2中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(画出一种即可);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,请在图3上画出示意图;
(3)在(2)的前提下,设∠C=x°,试求出x所有可能的值.
参考答案:
【答案】
(1)解:如图所示:

(2)解:如图所示:

(3)解:①当AD=AE时,
∵2x+x=30°+30°,
∴x=20°;
②当AD=DE时,
∵30°+30°+2x+x=180°,
∴x=40°
【解析】(1)45°自然想到等腰直角三角形,过底角一顶点作对边的高,发现形成一个等腰直角三角形和直角三角形.直角三角形斜边的中线可形成两个等腰三角形;第二种情形以一底角作为新等腰三角形的底角,则另一底角被分为45°和22.5°,再以22.5°分别作为等腰三角形的底角或顶角,易得其中作为底角时所得的三个三角形恰都为等腰三角形;
(2)用量角器,直尺标准作30°角,而后确定一边为BA,一边为BC,根据题意可以先固定BA的长,而后可确定D点,再分别考虑AD为等腰三角形的腰或者底边,兼顾A、E、C在同一直线上,易得2种三角形ABC;
(3)根据图形易得x的值;
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 的角平分线与边
的角平分线与边 交于点
交于点 ,
, 的角平分线交直线
的角平分线交直线 于点
于点 .
.(1)若点
 在四边形
在四边形 的内部,
的内部,①如图,若
 ,
, ,
, ,则
,则 _______°;
_______°;②如图,试探索
 、
、 、
、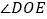 之间的数量关系,并将你的探索过程写下来.
之间的数量关系,并将你的探索过程写下来.(2)如图,若点
 是四边形
是四边形 的外部,请你直接写出
的外部,请你直接写出 、
、 、
、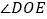 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2-x-2=0可通过因式分解化为(x-2)(x+1)=0,由基本事实得x-2=0或x+1=0,即方程的解为x=2或x=-1.
(1)、试利用上述基本事实,解方程:2x2-x=0:
(2)、若(x2+y2)(x2+y2-1)-2=0,求x2+y2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
-
科目: 来源: 题型:
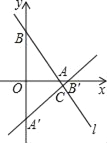
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣2x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
(1)求直线A′B′所对应的函数表达式.
(2)若直线A′B′与直线AB相交于点C,求△A′BC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<
 的解集(请直接写出答案).
的解集(请直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=4x2﹣4ax+a2﹣2a+2,
(1)当a=0,2,4时,请在同一直角坐标系中画出对应函数图象的顶点,并画出a=2 时的函数图象;
(2)证明当a取任意实数时,顶点在一条确定的直线上;
(3)求(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长.
相关试题

