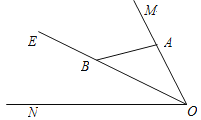
【题目】如图，已知∠MON＝80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合)，连接AC交射线OE于点D．当AB⊥OM，且△ADB有两个相等的角时，∠OAC的度数为______________．

参考答案：

【答案】10或25或40或115度

【解析】试题分析：①如图，当点D在线段OB上时，

若∠BAD=∠ABD，则∠OAC =40°

若∠BAD=∠BDA，则∠OAC =25°

若∠ADB=∠ABD，则∠OAC =10°

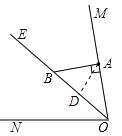
②如图，当点D在射线BE上时，因为∠ABE=130°，且三角形的内角和为180°，所以只有∠BAD=∠BDA，此时∠BAD=25°，因此∠OAC=90°+25°=115°．

综上可知，存在这样的∠OAC的度数10°、25°、40°、115°，使得△ADB中有两个相等的角.

故答案为：10°、25°、40°、115°.

关闭