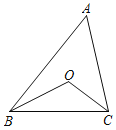
【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
参考答案:
【答案】40°
【解析】
先根据角平分线的定义得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,再根据三角形内角和定理得∠BOC+∠OBC+∠OCB=180°,则∠BOC=180°﹣
∠ACB,再根据三角形内角和定理得∠BOC+∠OBC+∠OCB=180°,则∠BOC=180°﹣![]() (∠ABC+∠ACB),由于∠ABC+∠ACB=180°﹣∠A,所以∠BOC=90°+
(∠ABC+∠ACB),由于∠ABC+∠ACB=180°﹣∠A,所以∠BOC=90°+![]() ∠A,然后把∠BOC=110°代入计算可得到∠A的度数.
∠A,然后把∠BOC=110°代入计算可得到∠A的度数.
解:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A,
∠A,
而∠BOC=110°,
∴90°+![]() ∠A=110°
∠A=110°
∴∠A=40°.
故答案为40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=
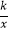 (k>0)上,则k的值为( )
(k>0)上,则k的值为( )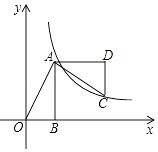
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形
 是半高三角形,且斜边
是半高三角形,且斜边 ,则它的周长等于_________.
,则它的周长等于_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
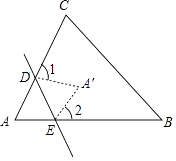
A.α
B.2α
C.180°﹣α
D.180°﹣2α -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( )
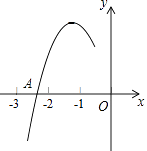
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
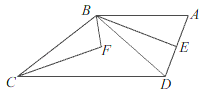
A. 115° B. 110° C. 105° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

相关试题

