【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( ) 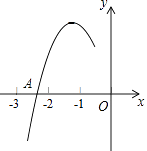
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:函数与x轴有两个交点,则b2﹣4ac>0,故①错误; 函数的对称轴是x=﹣1,即﹣ ![]() =﹣1,则b=2a,2a﹣b=0,故②正确;
=﹣1,则b=2a,2a﹣b=0,故②正确;
当x=1时,函数对应的点在x轴下方,则a+b+c<0,则③正确;
x1<x2 , 若同在对称轴的右侧,则y1>y2 , 则④错误.
所以正确的选项有②③两项,
故选B.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形
 是半高三角形,且斜边
是半高三角形,且斜边 ,则它的周长等于_________.
,则它的周长等于_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
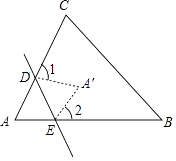
A.α
B.2α
C.180°﹣α
D.180°﹣2α -
科目: 来源: 题型:
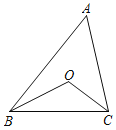
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
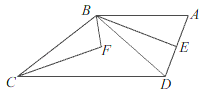
A. 115° B. 110° C. 105° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )

相关试题

