【题目】某校为打造书香校园,计划购进甲乙两种规格的书柜放置新购置的图书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需要资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个(其中乙种书柜的数量不少于甲种书柜的数量的![]() ).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
参考答案:
【答案】(1)甲种书柜单价为180元,乙种书柜的单价为240元;(2)W=-60m+4800当购买甲书柜12个,乙书柜8个时,资金最少.
【解析】
(1)设甲种书柜单价为x元,乙种书柜单价为y元,根据题意列出二元一次方程组,求解即可.
(2)设该校计划购进甲种书柜m个,则购进乙种书柜(20-m)个,根据“所需费用=甲种书柜费用+乙种书柜费用”列出关系式,根据“乙种书柜的数量不少于甲种书柜的数量的![]() ”列出不等式,求出不等式的解集;再利用一次函数的增减性确定方案即可.
”列出不等式,求出不等式的解集;再利用一次函数的增减性确定方案即可.
解:(1)设甲种书柜单价为x元,乙种书柜单价为y元,由题意得:
![]() 解得:
解得:![]()
答:甲种书柜单价为180元,乙种书柜单价为240元.
(2)设该校计划购进甲种书柜m个,则购进乙种书柜(20-m)个
由题意得:![]()
∵![]() ,解得:
,解得:![]()
∵![]()
∴W随m的增大而减小
∵![]()
∴当m=12时,W取最小值,最小值为![]() (元)
(元)
∴当购买甲种书柜12个,乙种书柜8个时,资金最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BD为一条对角线,∠ABD=90°,AD∥BC, AD=2BC,E为AD的中点,连接BE.

(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,则AC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(
 ,y1),点N(
,y1),点N( ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣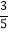 <a<﹣
<a<﹣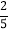 .其中正确结论有( )
.其中正确结论有( )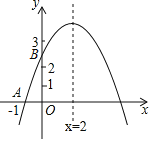
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
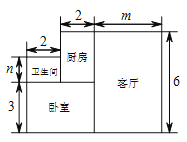
查看答案和解析>>【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含
 的代数式表示地面的总面积
的代数式表示地面的总面积  ;
;
(2)已知
 ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的  倍,如果铺
倍,如果铺  平方米地砖的平均费用为
平方米地砖的平均费用为  元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某购物网店在双十一期间实行打折促销活动,规定如下表:
次性购物不大于100元不打折,不大于300元但大于100元打九折,超过300元的部分打八折.
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该网店一次性购物
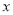 元,当
元,当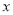 低于300元但大于100元时,他实际付款多少元?当
低于300元但大于100元时,他实际付款多少元?当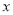 大于300元时,他实际付款多少元?(用含
大于300元时,他实际付款多少元?(用含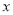 的式子表示)
的式子表示)(3)如果王老师两次购物货款合计820元,第一次购物的货款为
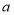 元
元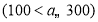 ,用含
,用含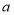 的式子表示两次购物王老师实际付款多少元?
的式子表示两次购物王老师实际付款多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】小华根据学习函数的经验,对函数
 的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
的图象与性质进行了研究,下面是小华的研究过程,请补充完成.(1)自变量
 的取值范围是全体实数,
的取值范围是全体实数, 与
与 的几组对应值列表如下:
的几组对应值列表如下:






4
5



m
2
1
0
n
2
3

其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;

(3)观察图象,写出该函数的两条性质;
(4)进一步研究函数图象发现:
①方程
 有 个实数根;
有 个实数根;②不等式
 的解集为 .
的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BE、CE 分别是∠ABC 和∠ACB 的平分线,过点 E 作 DF∥BC,交 AB 于 D,交 AC 于 F,若 AB=5,AC=4,则△ADF周长为________.

相关试题

