【题目】如图,在△ABC中,BE、CE 分别是∠ABC 和∠ACB 的平分线,过点 E 作 DF∥BC,交 AB 于 D,交 AC 于 F,若 AB=5,AC=4,则△ADF周长为________.

参考答案:
【答案】9
【解析】
根据平行线的性质和角平分线的定义得出BD=DE,EF=FC,进而解答即可.
∵DF∥BC,
∴∠DEB=∠EBC,∠FEC=∠ECB,
∵BE、CE分别是∠ABC和∠ACB的平分线,
∴∠DBE=∠EBC,∠FCE=∠ECB,
∴∠DBE=∠DEB,∠FEC=∠FCE,
∴BD=DE,EF=FC,
∴△ADF周长=AD+DF+AF=AD+AF+DE+EF=AD+AF+BD+FC=AB+AC=5+4=9,
故答案为:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为打造书香校园,计划购进甲乙两种规格的书柜放置新购置的图书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需要资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个(其中乙种书柜的数量不少于甲种书柜的数量的
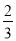 ).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】某购物网店在双十一期间实行打折促销活动,规定如下表:
次性购物不大于100元不打折,不大于300元但大于100元打九折,超过300元的部分打八折.
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该网店一次性购物
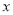 元,当
元,当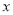 低于300元但大于100元时,他实际付款多少元?当
低于300元但大于100元时,他实际付款多少元?当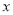 大于300元时,他实际付款多少元?(用含
大于300元时,他实际付款多少元?(用含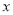 的式子表示)
的式子表示)(3)如果王老师两次购物货款合计820元,第一次购物的货款为
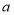 元
元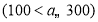 ,用含
,用含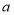 的式子表示两次购物王老师实际付款多少元?
的式子表示两次购物王老师实际付款多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】小华根据学习函数的经验,对函数
 的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
的图象与性质进行了研究,下面是小华的研究过程,请补充完成.(1)自变量
 的取值范围是全体实数,
的取值范围是全体实数, 与
与 的几组对应值列表如下:
的几组对应值列表如下:






4
5



m
2
1
0
n
2
3

其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;

(3)观察图象,写出该函数的两条性质;
(4)进一步研究函数图象发现:
①方程
 有 个实数根;
有 个实数根;②不等式
 的解集为 .
的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积是2平方厘米,△BCD 的面积是3平方厘米,△CDE的面积是3平方厘米,△DEF 的面积是4平方厘米,△EFG的面积是3平方厘米,△FGH的面积是5平方厘米,那么,△EFH的面积是______平方厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为3的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点C、E、F、G按逆时针排列),连接BF.
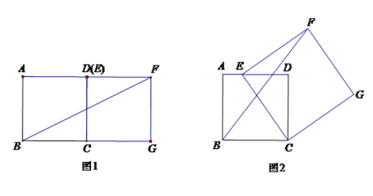
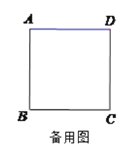
(1)如图1,当点E与点D重合时,BF的长为 ;
(2)如图2,当点E在线段AD上时,若AE=1,求BF的长;(提示:过点F作BC的垂线,交BC的延长线于点M,交AD的延长线于点N.)
(3)当点E在直线AD上时,若AE=4,请直接写出BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2
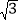 ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.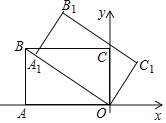
相关试题

