【题目】如图,在四边形ABCD中,BD为一条对角线,∠ABD=90°,AD∥BC, AD=2BC,E为AD的中点,连接BE.

(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,则AC的长为 .
参考答案:
【答案】(1)详见解析;(2)![]()
【解析】
(1)由DE=BC,AD∥BC,推出四边形BCDE是平行四边形,再证明BE=ED即可解决问题;
(2)利用“直角三角形中,30°角所对的直角边等于斜边的一半”逆定理,求得![]() ,进而求得
,进而求得![]() 和
和![]() ,再利用勾股定理即可解答.
,再利用勾股定理即可解答.
(1)证明:∵E为AD中点,AD=2BC ∴BC=ED
∵AD∥BC, ∴四边形BCDE是平行四边形
∵∠ABD=90°,AE=DE,∴ AD=2BE,
∴BE=ED ∴四边形BCDE是菱形
(2)
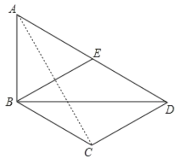
∵四边形BCDE是菱形,BC=1
∴AB=1 AD=2
∴![]()
∵AC平分∠BAD
∴![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=
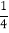 AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则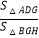 的值为( )
的值为( )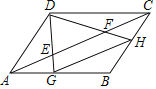
A.
 B.
B.  C.
C. 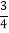 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一车间有
 人,第二车间比第一车间人数的
人,第二车间比第一车间人数的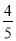 少30人,如果从第二车间调出10人到第一车间,那么:
少30人,如果从第二车间调出10人到第一车间,那么:(1)两个车间共有______人?
(2)调动后,第一车间的人数为______人,第二车的人数为______人.
(3)求调动后,第一车间的人数比第二车的人数多几人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送
 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位: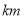 ):
):第
 批
批第
 批
批第
 批
批第
 批
批第
 批
批




(1)接送完第
 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?(2)若该出租车每千米耗油
 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?(3)若该出租车的计价标准为:行驶路程不超过
 收费
收费 元,超过
元,超过 的部分按每千米
的部分按每千米 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(
 ,y1),点N(
,y1),点N( ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣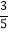 <a<﹣
<a<﹣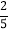 .其中正确结论有( )
.其中正确结论有( )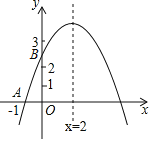
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
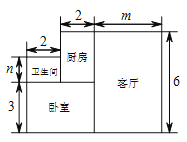
查看答案和解析>>【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含
 的代数式表示地面的总面积
的代数式表示地面的总面积  ;
;
(2)已知
 ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的  倍,如果铺
倍,如果铺  平方米地砖的平均费用为
平方米地砖的平均费用为  元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为打造书香校园,计划购进甲乙两种规格的书柜放置新购置的图书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需要资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个(其中乙种书柜的数量不少于甲种书柜的数量的
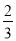 ).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
相关试题

