【题目】阅读材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式![]() 的最小值.方法如下:
的最小值.方法如下:
解:![]()
![]()
![]()
∵![]() ,得
,得![]() ,
,
∴代数式![]() 的最小值是4.
的最小值是4.
请根据上述材料,解决下列问题:
(1)求代数式![]() 的最小值.
的最小值.
(2)用配方法求代数式![]() 的最值.
的最值.
参考答案:
【答案】(1)14;(2)最大值14;
【解析】
(1)仿照阅读材料、利用配方法把原式化为完全平方式与一个数的和的形式,根据偶次方的非负性解答;
(2)利用配方法把原式进行变形,根据偶次方的非负性解答即可.
(1)∵x2+6x5=x2+6x+914=(x+3)214,由(x+3)20,得(x+3)21414;
∴代数式x2+6x5的最小值是14;
(2)a24a+10=a24a4+14=(a+2)2+14,
∵(a+2)20,
∴(a+2)2+1414,
∴代数式a24a+10有最大值,最大值为14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
 x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 (x>0)的图象相交于C点.
(x>0)的图象相交于C点.(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数
 (x>0)的关系式.
(x>0)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=20°,∠ABC=30°.
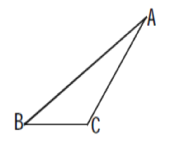
(1)画出BC边上的高AD和角平分线AE;
(2)求∠EAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是△ABC的三边长,且满足a2+2ab=c2+2bc,试判断这个三角形的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,OE平分
,OE平分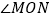 ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点 、B、C不与点O重合
、B、C不与点O重合 ,连接AC交射线OE于点
,连接AC交射线OE于点 设
设 .
.
 如图1,若
如图1,若 ,则
,则 的度数是______;
的度数是______; 当
当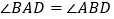 时,
时, ______;当
______;当 时,
时, ______.
______. 如图2,若
如图2,若 ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
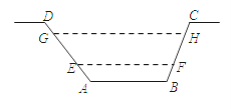
A. 1.2 B. 1.1 C. 0.8 D. 2.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:
 ≈1.4)( )
≈1.4)( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

