【题目】如图为![]() 和一圆的重迭情形,此圆与直线
和一圆的重迭情形,此圆与直线![]() 相切于
相切于![]() 点,且与
点,且与![]() 交于另一点
交于另一点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的度数为何( )
的度数为何( )
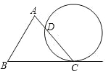
A. 50° B. 60° C. 100° D. 120°
参考答案:
【答案】C
【解析】
设圆心为O,连接CO,并延长交⊙O于点E,连接DE,DO.先根据三角形的内角和定理求得∠C的度数,再根据圆周角定理和切线的性质得到∠COD=2∠ACB,即可得出结论.
设圆心为O,连接CO,并延长交⊙O于点E,连接DE,DO.
∵∠A=70°,∠B=60°,∴∠ACB=50°.
∵此圆与直线BC相切于C点,∴∠BCE=90°,∴∠ACB+∠ACE=90°.
∵CE为直径,∴∠EDC=90°,∴∠DCE+∠E=90°,∴∠ACB=∠E.
∵∠COD=2∠E,∴∠COD=2∠ACB=100°,∴弧CD的度数=∠COD=100°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,则CE2+CF2 的值为( )

A.36B.9C.6D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
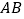 是
是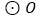 的直径,延长
的直径,延长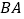 至点
至点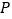 ,过点
,过点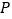 作
作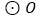 的切线
的切线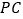 ,切点为
,切点为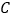 ,过点
,过点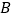 向
向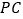 的延长线作垂线
的延长线作垂线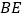 交该延长线于点
交该延长线于点 ,
,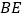 交
交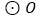 于点
于点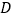 ,已知
,已知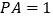 ,
,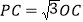 .
.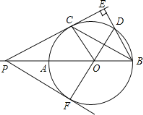
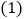 求
求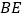 的长;
的长;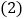 连结
连结 ,延长
,延长 交
交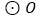 于
于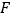 ,连结
,连结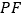 .
.①求
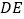 的长;
的长;②求证:
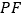 是
是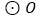 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
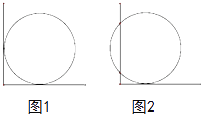
A. 25cm B. 30cm C. 50cm D. 60cm
-
科目: 来源: 题型:
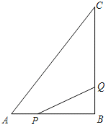
查看答案和解析>>【题目】如图所示,
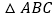 中,
中,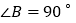 ,
,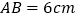 ,
,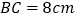 .
.
 点
点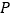 从点
从点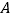 开始沿
开始沿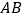 边向
边向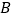 以
以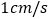 的速度移动,点
的速度移动,点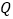 从
从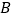 点开始沿
点开始沿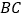 边向点
边向点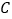 以
以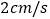 的速度移动.如果
的速度移动.如果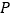 、
、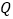 分别从
分别从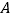 ,
,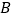 同时出发,线段
同时出发,线段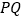 能否将
能否将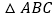 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.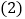 若
若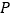 点沿射线
点沿射线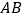 方向从
方向从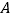 点出发以
点出发以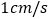 的速度移动,点
的速度移动,点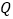 沿射线
沿射线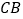 方向从
方向从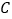 点出发以
点出发以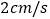 的速度移动,
的速度移动,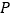 、
、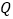 同时出发,问几秒后,
同时出发,问几秒后,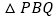 的面积为
的面积为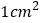 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
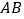 为
为 的直径,
的直径, ,
, 为
为 上的两点,
上的两点, 平分
平分 ,
, 于
于 .
. 求证:
求证: 为
为 的切线;
的切线; 过点
过点 作
作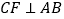 于
于 ,如图
,如图 ,判断
,判断 和
和 ,
, 之间的数量关系,并证明之;
之间的数量关系,并证明之; 若
若 ,
, ,求图中阴影部分的面积.
,求图中阴影部分的面积.
相关试题

