【题目】如图,![]() 是
是![]() 的直径,延长
的直径,延长![]() 至点
至点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,切点为
,切点为![]() ,过点
,过点![]() 向
向![]() 的延长线作垂线
的延长线作垂线![]() 交该延长线于点
交该延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
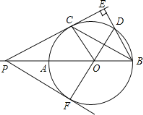
![]() 求
求![]() 的长;
的长;
![]() 连结
连结![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
①求![]() 的长;
的长;
②求证:![]() 是
是![]() 的切线.
的切线.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②见解析
;②见解析
【解析】
(1)在直角△OPC中,利用勾股定理即可得到圆的半径长,然后利用相似三角形的性质求得BE的长;
(2)①证明△OBD是等边三角形,即可求得DE的长;
②首先证明△OPC≌△OPF,根据切线的判定定理即可证得.
(1)设圆的半径是r,则OP=PA+r=1+r,OC=r,PC=![]() r.
r.
∵PC是圆的切线,∴∠PCO=90°,在直角△PCO中,PC2+OC2=OP2,即(![]() r)2+r2=(1+r)2,解得:r=1或r=﹣
r)2+r2=(1+r)2,解得:r=1或r=﹣![]() (舍去负值).
(舍去负值).
在直角△OPC中,cos∠POC=![]() =
=![]() ,∴∠POC=60°.
,∴∠POC=60°.
∵∠PCO=90°,BE⊥BC,∴BE∥OC,∴△OPC∽△BPE,∠OBD=∠POC=60°,∴![]() =
=![]() =
=![]() ,∴BE=
,∴BE=![]() OC=
OC=![]() ;
;
(2)①在△OBD中,OB=OD,∠OBD=60°,∴△OBD是等边三角形,BD=OB=1,∠BOD=60°,∴DE=BE﹣BD=![]() ﹣1=
﹣1=![]() ;
;
②∵∠POC=60°,∠BOD=60°,∴∠POF=60°,∴∠POC=∠POF.在△OPC和△OPF中,∵ ,△OPC≌△OPF(SAS),∴∠OFP=∠OCP=90°,∴PF是⊙O的切线.
,△OPC≌△OPF(SAS),∴∠OFP=∠OCP=90°,∴PF是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,则CE2+CF2 的值为( )

A.36B.9C.6D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为
 和一圆的重迭情形,此圆与直线
和一圆的重迭情形,此圆与直线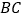 相切于
相切于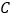 点,且与
点,且与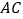 交于另一点
交于另一点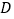 .若
.若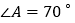 ,
, ,则
,则 的度数为何( )
的度数为何( )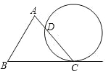
A. 50° B. 60° C. 100° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
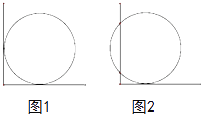
A. 25cm B. 30cm C. 50cm D. 60cm
-
科目: 来源: 题型:
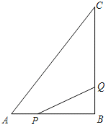
查看答案和解析>>【题目】如图所示,
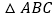 中,
中,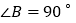 ,
,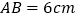 ,
,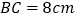 .
.
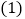 点
点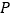 从点
从点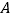 开始沿
开始沿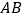 边向
边向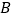 以
以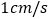 的速度移动,点
的速度移动,点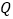 从
从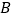 点开始沿
点开始沿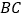 边向点
边向点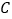 以
以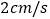 的速度移动.如果
的速度移动.如果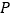 、
、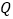 分别从
分别从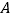 ,
,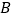 同时出发,线段
同时出发,线段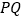 能否将
能否将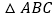 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.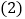 若
若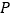 点沿射线
点沿射线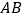 方向从
方向从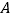 点出发以
点出发以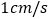 的速度移动,点
的速度移动,点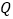 沿射线
沿射线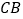 方向从
方向从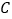 点出发以
点出发以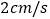 的速度移动,
的速度移动,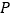 、
、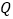 同时出发,问几秒后,
同时出发,问几秒后,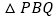 的面积为
的面积为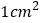 ?
?
相关试题

