【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
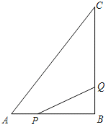
![]() 点
点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
![]() 若
若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() 、
、![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
参考答案:
【答案】(1) 线段![]() 不能将
不能将![]() 分成面积相等的两部分;(2) 经过
分成面积相等的两部分;(2) 经过![]() 秒、
秒、![]() 秒或
秒或![]() 秒后,
秒后,![]() 的面积为
的面积为![]() .
.
【解析】
(1)设经过x秒,线段PQ能否将△ABC分成面积相等的两部分,根据面积之间的等量关系和判别式即可求解;
(2)分三种情况:①点P在线段AB上,点Q在线段CB上(0<t≤4);②点P在线段AB上,点Q在线段CB上(4<t≤6);③点P在射线AB上,点Q在射线CB上(t>6);进行讨论即可求解.
(1)设经过x秒,线段PQ能将△ABC分成面积相等的两部分
由题意知:AP=x,BQ=2x,则BP=6﹣x,∴![]() (6﹣x)2x=
(6﹣x)2x=![]() ×
×![]() ×6×8,∴x2﹣6x+12=0.
×6×8,∴x2﹣6x+12=0.
∵b2﹣4ac<0,此方程无解,∴线段PQ不能将△ABC分成面积相等的两部分;
(2)设t秒后,△PBQ的面积为1.分三种情况讨论:
①当点P在线段AB上,点Q在线段CB上时,此时0<t≤4.
由题意知:![]() (6﹣t)(8﹣2t)=1,整理得:t2﹣10t+23=0,解得:t1=5+
(6﹣t)(8﹣2t)=1,整理得:t2﹣10t+23=0,解得:t1=5+![]() (不合题意,应舍去),t2=5﹣
(不合题意,应舍去),t2=5﹣![]()
②当点P在线段AB上,点Q在线段CB的延长线上时,此时4<t≤6,由题意知:![]() (6﹣t)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=t2=5.
(6﹣t)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=t2=5.
③当点P在线段AB的延长线上,点Q在线段CB的延长线上时,此时t>6,由题意知:![]() (t﹣6)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=5+
(t﹣6)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=5+![]() ,t2=5﹣
,t2=5﹣![]() (不合题意,应舍去).
(不合题意,应舍去).
综上所述:经过5﹣![]() 秒、5秒或5+
秒、5秒或5+![]() 秒后,△PBQ的面积为1.
秒后,△PBQ的面积为1.
-
科目: 来源: 题型:
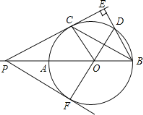
查看答案和解析>>【题目】如图,
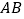 是
是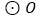 的直径,延长
的直径,延长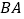 至点
至点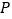 ,过点
,过点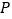 作
作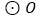 的切线
的切线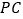 ,切点为
,切点为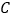 ,过点
,过点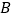 向
向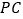 的延长线作垂线
的延长线作垂线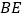 交该延长线于点
交该延长线于点 ,
,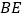 交
交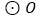 于点
于点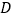 ,已知
,已知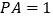 ,
,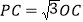 .
.
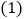 求
求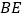 的长;
的长; 连结
连结 ,延长
,延长 交
交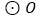 于
于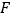 ,连结
,连结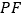 .
.①求
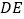 的长;
的长;②求证:
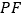 是
是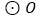 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为
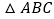 和一圆的重迭情形,此圆与直线
和一圆的重迭情形,此圆与直线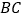 相切于
相切于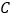 点,且与
点,且与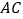 交于另一点
交于另一点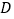 .若
.若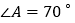 ,
, ,则
,则 的度数为何( )
的度数为何( )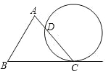
A. 50° B. 60° C. 100° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
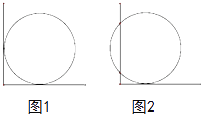
A. 25cm B. 30cm C. 50cm D. 60cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
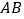 为
为 的直径,
的直径, ,
, 为
为 上的两点,
上的两点, 平分
平分 ,
, 于
于 .
. 求证:
求证: 为
为 的切线;
的切线; 过点
过点 作
作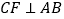 于
于 ,如图
,如图 ,判断
,判断 和
和 ,
, 之间的数量关系,并证明之;
之间的数量关系,并证明之; 若
若 ,
, ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.

(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
相关试题

