【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使之是由△ABC平移后得到,且A与A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得的;
(3)将△ABC绕点A逆时针旋转一定角度,使得AB落在(2)中的线段AD的位置,请作出旋转后的三角形,并求在这一旋转过程中△ABC扫过的面积.

参考答案:
【答案】(1)图见解析;(2)图见解析,AD可看作由AB绕A点逆时针旋转90°而得;(3)图见解析;△ABC扫过的面积为![]() π+7.5
π+7.5
【解析】
(1)根据网格结构找出点A、B、C平移后对应点进而得出答案;
(2)根据网格结构找出点B的对应点的位置即可得出答案;
(3)根据图形可知,扫过的面积是以A点为圆心,AC长为半径的扇形的面积加上△ABC的面积,据此进一步列式求解即可.

(1)如图所示:△A1B1C1即为所求;
(2)如图所示:AD即为所求,且可看作由AB绕A点逆时针旋转90°而得;
(3)如图所示,△ADE即为所求作的三角形,
根据勾股定理,AC=![]() ,
,
∴扇形AEC的面积=![]() =
=![]() π,
π,
△ABC的面积=6×4![]() ×3×4
×3×4![]() ×1×3
×1×3![]() ×6×3=7.5,
×6×3=7.5,
所以,△ABC扫过的面积为![]() π+7.5.
π+7.5.
-
科目: 来源: 题型:
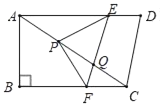
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AD∥BC,AD=AC,AB=6,BC=8.点P以每秒5个单位长度由点A沿线段AC运动;同时,线段EF以相同的速度由CD出发沿DA方向平移,与AC交于点Q,连结PE,PF.当点F与点B重合时,停止所有运动,设P运动时间为t秒.
(1)求证:△APE≌△CFP.
(2)当t<1时,若△PEF为直角三角形,求t的值.
(3)作△PEF的外接圆⊙O.
①当⊙O只经过线段AC的一个端点时,求t的值.
②作点P关于EF的对称点P′,当P′落在CD上时,请直接写出线段CP′的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△DEF均为等腰直角三角形,AB=2,DE=1,E、B、F、C在同一条直线上,开始时点B与点F重合,让△DEF沿直线BC向右移动,最后点C与点E重合,设两三角形重合面积为y,点F移动的距离为x,则y关于x的大致图象是( )

A.
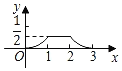 B.
B.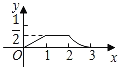
C.
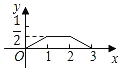 D.
D.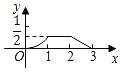
-
科目: 来源: 题型:
查看答案和解析>>【题目】若反比例函数y=﹣
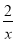 的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______.
的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式,探究其中的规律:①
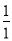 +
+ ﹣1=
﹣1= ,②
,②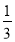 +
+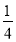 ﹣
﹣ =
=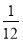 ,③
,③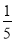 +
+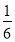 ﹣
﹣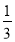 =
=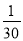 ,④
,④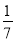 +
+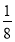 ﹣
﹣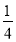 =
=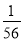 ,….
,….(1)按以上规律写出第⑧个等式:_______;
(2)猜想并写出第n个等式:_________;
(3)请证明猜想的正确性.
-
科目: 来源: 题型:
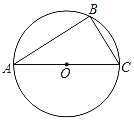
查看答案和解析>>【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2
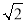 .
.(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中
 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;(4)身高在
 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
相关试题

