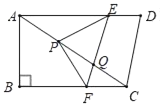
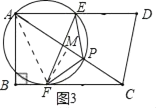
【题目】如图,四边形ABCD中,∠B=90°,AD∥BC,AD=AC,AB=6,BC=8.点P以每秒5个单位长度由点A沿线段AC运动;同时,线段EF以相同的速度由CD出发沿DA方向平移,与AC交于点Q,连结PE,PF.当点F与点B重合时,停止所有运动,设P运动时间为t秒.
(1)求证:△APE≌△CFP.
(2)当t<1时,若△PEF为直角三角形,求t的值.
(3)作△PEF的外接圆⊙O.
①当⊙O只经过线段AC的一个端点时,求t的值.
②作点P关于EF的对称点P′,当P′落在CD上时,请直接写出线段CP′的长.
参考答案:
【答案】(1)详见解析;(2)t=![]() ;(3)①t的值为
;(3)①t的值为![]() 和
和![]() ;②
;②![]()
【解析】
(1)利用勾股定理求出AD=AC=10,根据AD∥BC得到∠EAC=∠ACF,再根据AE=CP=10﹣5t即可证得结论;
(2)过点P作PM⊥AD于点M,延长MP交BC于N,证明四边形ABNM是矩形得到△PNC∽△ABC,求出PM=MN﹣PN=3t,NF=NC﹣FC=8﹣9t,由△APE≌△CFP得到PE=PF,由△EPF为直角三角形得到∠MEP=∠NPF,由此证明△EMP≌△PNF得到PM=NF,建立等式求出t;
(3)①分两种情况:当⊙O过点C时,连接CE,过点E作EM⊥AC于M.根据PE=PF证得∠PCE=∠PCF,再求出CE=AE=10﹣5t,CM=AM=![]() AC=5,根据cos∠PCE=cos∠PCF即可求出t;当⊙O过点A时可得AF=FC=5t,根据cos∠PCE=cos∠PCF即可求出t;
AC=5,根据cos∠PCE=cos∠PCF即可求出t;当⊙O过点A时可得AF=FC=5t,根据cos∠PCE=cos∠PCF即可求出t;
②过点C作CH⊥AD于H,连接PP',交EF于点G,证明△PGQ∽△PP'C求出PQ,根据对顶角的性质及平行线的性质求出CQ=CF求出t,利用勾股定理求出EF,计算出FG、FQ求出QG即可求出答案.
解:(1)证明:∵AD∥BC,EF∥CD
∴四边形CDEF是平行四边形,∠EAC=∠ACF
∴ED=FC=5t
∵∠B=90°,AB=6,BC=8
∴AD=AC=![]() =10
=10
∴AE=CP=10﹣5t
在△APE与△CFP中,

∴△APE≌△CFP(SAS)
(2)过点P作PM⊥AD于点M,延长MP交BC于N,
∴∠EMP=∠PNF=90°,MN∥AB
∴∠MEP+∠MPE=90°,四边形ABNM是矩形,△PNC∽△ABC
∴MN=AB=6,![]()
∴PN=6﹣3t,NC=8﹣4t
∴PM=MN﹣PN=3t,NF=NC﹣FC=8﹣9t
∵△APE≌△CFP
∴PE=PF,
∵△EPF为直角三角形
∴∠EPF=90°
∴∠MPE+∠NPF=90°
∴∠MEP=∠NPF
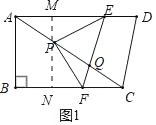
在△EMP与△PNF中,
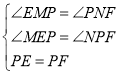
∴△EMP≌△PNF(AAS)
∴PM=NF
∴3t=8﹣9t
解得:t=![]()
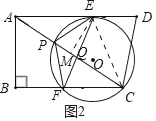
(3)①(ⅰ)当⊙O过点C时(如图2),连接CE,过点E作EM⊥AC于M.
∵PE=PF,
∴![]()
∴∠PCE=∠PCF
∵AD∥BC
∴∠PCF=∠DAC
∴∠PCE=∠DAC,
∴CE=AE=10﹣5t,CM=AM=![]() AC=5
AC=5
∵cos∠PCE=cos∠PCF
∴![]() 即
即![]()
解得:t=![]()
(ⅱ)当⊙O过点A时(如图3),可得AF=FC=5t
∴cos∠FAP=cos∠PCF
∴![]() 即
即![]()
解得:t=![]()
综上所述,t的值为![]() 和
和![]()
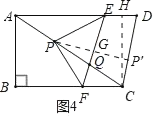
②过点C作CH⊥AD于H,连接PP',交EF于点G
∴G为PP'和EF的中点
∵P'在CD上,EF∥CD
∴△PGQ∽△PP'C
∴![]() =
=![]()
∴PQ=CQ=![]() PC=
PC=![]()
∵AC=AD
∴∠ACD=∠D
∴∠AQE=∠ACD=∠D=∠AEQ
∵∠AQE=∠CQF,∠AEQ=∠CFQ
∴∠CQF=∠CFQ
∴CQ=CF
∴![]()
解得:t=![]()
∴CF=![]() ,AE=10﹣
,AE=10﹣![]() =
=![]()
∴![]() ,即FQ=
,即FQ=![]() EF
EF
∵∠CHD=90°,CH=AB=6,DH=AD﹣AH=AD﹣BC=2
∴EF=CD=![]()
∴FG=![]() EF=
EF=![]() ,FQ=
,FQ=![]() EF=
EF=![]()
∴GQ=FG﹣FQ=![]()
∴CP'=2GQ=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

-
科目: 来源: 题型:
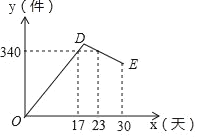
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
-
科目: 来源: 题型:
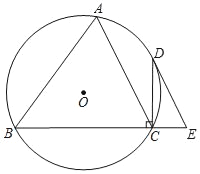
查看答案和解析>>【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
-
科目: 来源: 题型:
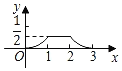
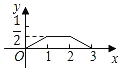
查看答案和解析>>【题目】如图,已知△ABC和△DEF均为等腰直角三角形,AB=2,DE=1,E、B、F、C在同一条直线上,开始时点B与点F重合,让△DEF沿直线BC向右移动,最后点C与点E重合,设两三角形重合面积为y,点F移动的距离为x,则y关于x的大致图象是( )

A.
 B.
B.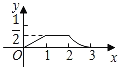
C.
 D.
D.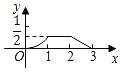
-
科目: 来源: 题型:
查看答案和解析>>【题目】若反比例函数y=﹣
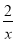 的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______.
的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使之是由△ABC平移后得到,且A与A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得的;
(3)将△ABC绕点A逆时针旋转一定角度,使得AB落在(2)中的线段AD的位置,请作出旋转后的三角形,并求在这一旋转过程中△ABC扫过的面积.

相关试题

