【题目】如图,已知△ABC和△DEF均为等腰直角三角形,AB=2,DE=1,E、B、F、C在同一条直线上,开始时点B与点F重合,让△DEF沿直线BC向右移动,最后点C与点E重合,设两三角形重合面积为y,点F移动的距离为x,则y关于x的大致图象是( )

A.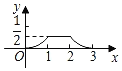 B.
B.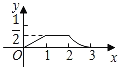
C.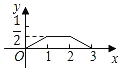 D.
D.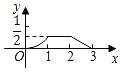
参考答案:
【答案】A
【解析】
根据题意,结合图形分①当![]() 时、②当
时、②当![]() 时与③当
时与③当![]() 时三种情况,分别求出各自情况下
时三种情况,分别求出各自情况下![]() 与
与![]() 的情况,据此进一步判断具体的函数图象即可.
的情况,据此进一步判断具体的函数图象即可.
根据题意,得:△DEF移动的过程中,阴影部分总为等腰直角三角形,
①如图,

当![]() 时,重合部分的直角边长为
时,重合部分的直角边长为![]() ,
,
则![]() ;
;
②如图,
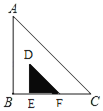
当![]() 时,重合部分的直角边长为1,
时,重合部分的直角边长为1,
则![]() ;
;
③如图,
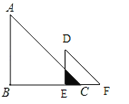
当![]() 时,重合部分的直角边长为
时,重合部分的直角边长为![]() ,
,
则![]() ,
,
由以上分析可知:这个分段函数的图象左边为开口向上的抛物线一部分,中间为直线的一部分,右边为开口向上的抛物线一部分.
故选:A.
-
科目: 来源: 题型:
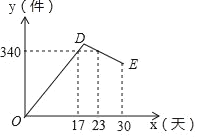
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
-
科目: 来源: 题型:
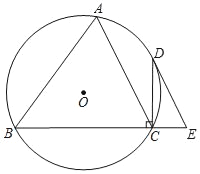
查看答案和解析>>【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
-
科目: 来源: 题型:
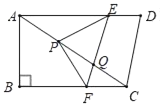
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AD∥BC,AD=AC,AB=6,BC=8.点P以每秒5个单位长度由点A沿线段AC运动;同时,线段EF以相同的速度由CD出发沿DA方向平移,与AC交于点Q,连结PE,PF.当点F与点B重合时,停止所有运动,设P运动时间为t秒.
(1)求证:△APE≌△CFP.
(2)当t<1时,若△PEF为直角三角形,求t的值.
(3)作△PEF的外接圆⊙O.
①当⊙O只经过线段AC的一个端点时,求t的值.
②作点P关于EF的对称点P′,当P′落在CD上时,请直接写出线段CP′的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若反比例函数y=﹣
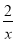 的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______.
的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使之是由△ABC平移后得到,且A与A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得的;
(3)将△ABC绕点A逆时针旋转一定角度,使得AB落在(2)中的线段AD的位置,请作出旋转后的三角形,并求在这一旋转过程中△ABC扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式,探究其中的规律:①
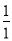 +
+ ﹣1=
﹣1= ,②
,②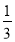 +
+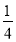 ﹣
﹣ =
=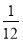 ,③
,③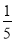 +
+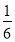 ﹣
﹣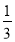 =
=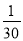 ,④
,④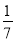 +
+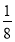 ﹣
﹣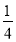 =
=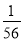 ,….
,….(1)按以上规律写出第⑧个等式:_______;
(2)猜想并写出第n个等式:_________;
(3)请证明猜想的正确性.
相关试题

