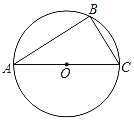
【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2![]() .
.
(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
参考答案:
【答案】(1)见解析;(2)BE=1+![]() .
.
【解析】
(1)首先根据直径所对的圆周角为90°可知∠ABC=90°,由此可知要使∠ABE为45°,只要画出∠ABC的角平分线即可,据此按照角平分线的作图方法画图即可;
(2)过点C作CF⊥BE,垂足为F,连接CE,首先根据AC为直径得出∠ABC=90°,然后利用“30°角所对的直角边为斜边一半”得出BC的长,然后在Rt△BFC中利用三角函数求出CF,由此进一步得出BF,最后在Rt△EFC中再次根据三角函数求出EF,由此即可得出答案.
(1)如图,∠ABE即为所求;
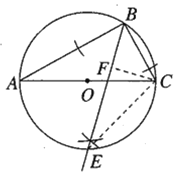
(2)过点C作CF⊥BE,垂足为F,连接CE,
∵∠A=30°,
∴∠BEC=30°,
∵AC为直径,
∴∠ABC=90°,
由(1)可知∠ABE=45°,
∴∠EBC=45°,
在Rt△ABC中,∵∠A=30°,AC=![]() ,
,
∴BC=![]() ,
,
在Rt△BFC中,sin∠FBC=![]() ,
,
∴CF=1,
∵∠EBC=45°,CF⊥BE,
∴∠BCF=45°,
∴BF=CF=1,
在Rt△EFC中,tan∠BEC=![]() ,
,
∴EF=![]() ,
,
∴BE=BF+EF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若反比例函数y=﹣
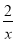 的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______.
的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=﹣x+m的图象上,则m的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使之是由△ABC平移后得到,且A与A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得的;
(3)将△ABC绕点A逆时针旋转一定角度,使得AB落在(2)中的线段AD的位置,请作出旋转后的三角形,并求在这一旋转过程中△ABC扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式,探究其中的规律:①
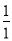 +
+ ﹣1=
﹣1= ,②
,②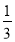 +
+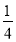 ﹣
﹣ =
=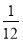 ,③
,③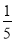 +
+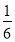 ﹣
﹣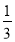 =
=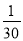 ,④
,④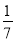 +
+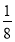 ﹣
﹣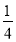 =
=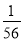 ,….
,….(1)按以上规律写出第⑧个等式:_______;
(2)猜想并写出第n个等式:_________;
(3)请证明猜想的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中
 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;(4)身高在
 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率. -
科目: 来源: 题型:
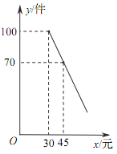
查看答案和解析>>【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
-
科目: 来源: 题型:
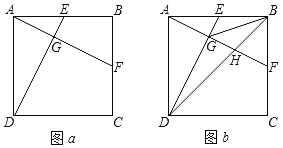
查看答案和解析>>【题目】如图a,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.
(1)求证:AF⊥DE;
(2)如图b,连接BG,BD,BD交AF于点H.
①求证:GB2=GAGD;
②若AB=10,求三角形GBH的面积.
相关试题

