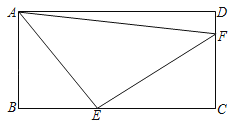
【题目】如图,在长方形ABCD中,点E在BC上,点F在CD上,且满足BE=CF=a,AB=EC=b.
(1)判断△AEF的形状,并证明你的结论;
(2)请用含a,b的代数式表示△AEF的面积;
(3)当△ABE的面积为24,BC长为14时,求△ADF的面积.
参考答案:
【答案】(1)△AEF是等腰直角三角形,理由详见解析;(2)![]() (a2+b2);(3)14.
(a2+b2);(3)14.
【解析】
(1)证明△ABE≌△ECF(SAS),得出AE=EF,∠BAE=∠CEF,证出∠AEF=90°,即可得出△AEF是等腰直角三角形;
(2)由勾股定理得出AE2=AB2+BE2=a2+b2,由三角形面积公式即可得出答案;
(3)求出ab=48,由题意得出(a+b)2=142,求出a2+b2=100,得出(a﹣b)2=4,证出b﹣a=2,由三角形面积公式即可得出答案.
(1)△AEF是等腰直角三角形,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°,AD=BC=a+b,
在△ABE和△ECF中,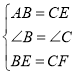 ,
,
∴△ABE≌△ECF(SAS),
∴AE=EF,∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴△AEF是等腰直角三角形;
(2)∵∠B=90°,BE=CF=a,AB=CE=b,
∴AE2=AB2+BE2=a2+b2,
∴△AEF的面积=![]() AE×EF=
AE×EF=![]() AE2=
AE2=![]() (a2+b2);
(a2+b2);
(3)∵△ABE的面积=24=![]() ab,
ab,
∴ab=48,
∵BC=14,
∴a+b=14,
∴(a+b)2=142,
∴a2+2ab+b2=196,
∴a2+b2=100,
∴a2﹣2ab+b2=100﹣96=4,
即(a﹣b)2=4,
∵CD>F,
∴b>a,
∴b﹣a=2,
∴△ADF的面积=![]() AD×DF=
AD×DF=![]() BC×(b﹣a)=
BC×(b﹣a)=![]() ×14×2=14.
×14×2=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年2月3日至2019年2月20日,“第一届”成都金沙太阳节在金沙遗址博物馆成功举办,用世界文明展览,主题灯展,园林花艺,美食演绎等一系列文化活动,与玛雅这一著名的中美洲文明结下不解之缘,为成都人打造了一个博物馆里的“文化年”.春节当天,小杰于下午
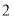 点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离
点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离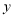 (千米)与他离家的时间
(千米)与他离家的时间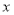 (小时)之间的图像.根据图像,完成下面的问题:
(小时)之间的图像.根据图像,完成下面的问题: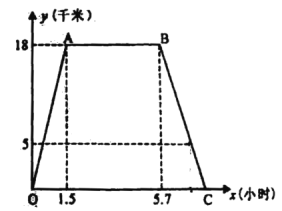
(1)小杰家距金沙遗址博物馆 千米,他乘车去金沙遗址博物馆的速度是 千米/小时;
(2)已知晚上
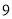 点时,小杰距家
点时,小杰距家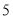 千米,请通过计算说明他何时才能回到家?
千米,请通过计算说明他何时才能回到家?(3)请直接写出小杰回家过程中
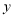 与
与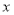 的关系式.
的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E.若AD=8cm,则OE的长为( )
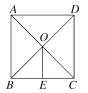
A. 3cm B. 4cm C. 6cm D. 8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在上海的小明一家将于5月1日到苏州进行自驾游,准备将行程分为上午和下午,上午的备选地点为:A-重元寺、B-苏州乐园、C-观前街,下午的备选地点为:D-李公堤、E-金鸡湖摩天轮公园.
(1)请用画树状图或列表的方法写出小明家所有可能的游玩方式(用字母表示即可);
(2)求小明一家恰好整天在工业园区游玩的概率.(提示:重元寺、李公堤、金鸡湖摩天轮公园在工业园区)
-
科目: 来源: 题型:
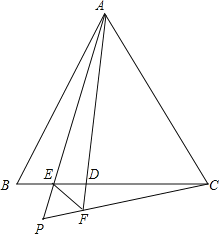
查看答案和解析>>【题目】如图,在△ABC中,点D为线段BC上一点(不含端点),AP平分∠BAD交BC于E,PC与AD的延长线交于点F,连接EF,且∠PEF=∠AED.
(1)求证:AB=AF;
(2)若△ABC是等边三角形.
①求∠APC的大小;
②想线AP,PF,PC之间满足怎样的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.
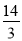 C.3D.
C.3D.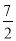
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
相关试题

