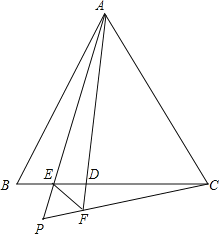
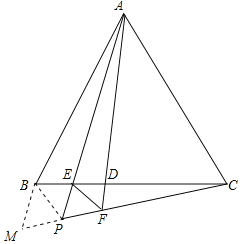
【题目】如图,在△ABC中,点D为线段BC上一点(不含端点),AP平分∠BAD交BC于E,PC与AD的延长线交于点F,连接EF,且∠PEF=∠AED.
(1)求证:AB=AF;
(2)若△ABC是等边三角形.
①求∠APC的大小;
②想线AP,PF,PC之间满足怎样的数量关系,并证明.
参考答案:
【答案】(1)详见解析;(2)①60°;②AP=PF+PC,理由详见解析.
【解析】
(1)由已知证出∠AEB=∠AEF,∠BAP=∠FAP,证明△AEB≌△AEF,即可得出AB=AF;
(2)①由等边三角形的性质得出AB=AC=BC,∠BAC=60°,证出AF=AC,设∠BAP=∠FAP=x,则∠FAC=60°﹣2x,求出∠AFC=x+60°,由三角形的外角性质得出∠AFC=∠FAP+∠APC=x+∠APC,即可得出结果;
②延长CP至点M,使PM=PF,连接BM、BP,先证明△APB≌△APF,得出∠APC=∠APB=60°,PB=PF,得出∠BPM=60°,PM=PB,得出△BPM是等边三角形,得出BP=BM,∠ABP=∠CBM=60°+∠PBC,再证明△ABP≌△CBM,即可得出结论.
(1)证明:∵∠PEF=∠AED,
∴180°﹣∠PEF=180°﹣∠AED,
∴∠AEB=∠AEF,
∵AP平分∠BAD,
∴∠BAP=∠FAP,
在△AEB和△AEF中,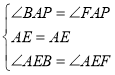 ,
,
∴△AEB≌△AEF(ASA),
∴AB=AF;
(2)解:①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵AB=AF,
∴AF=AC,
设∠BAP=∠FAP=x,则∠FAC=60°﹣2x,
在△ACF中,∠AFC=![]() [180°﹣(60°﹣2x)]=x+60°,
[180°﹣(60°﹣2x)]=x+60°,
又∵∠AFC=∠FAP+∠APC=x+∠APC,
∴∠APC=60°;
②AP=PF+PC,理由如下:
延长CP至点M,使PM=PF,连接BM、BP,如图所示:
在△APB和△APF中,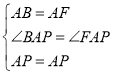 ,
,
∴△APB≌△APF(SAS),
∴∠APC=∠APB=60°,PB=PF,
∴∠BPM=60°,PM=PB,
∴△BPM是等边三角形,
∴BP=BM,∠ABP=∠CBM=60°+∠PBC,
在△ABP和△CBM中,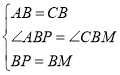 ,
,
∴△ABP≌△CBM(SAS),
∴AP=CM=PM+PC=PF+PC.
-
科目: 来源: 题型:
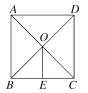
查看答案和解析>>【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E.若AD=8cm,则OE的长为( )
A. 3cm B. 4cm C. 6cm D. 8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在上海的小明一家将于5月1日到苏州进行自驾游,准备将行程分为上午和下午,上午的备选地点为:A-重元寺、B-苏州乐园、C-观前街,下午的备选地点为:D-李公堤、E-金鸡湖摩天轮公园.
(1)请用画树状图或列表的方法写出小明家所有可能的游玩方式(用字母表示即可);
(2)求小明一家恰好整天在工业园区游玩的概率.(提示:重元寺、李公堤、金鸡湖摩天轮公园在工业园区)
-
科目: 来源: 题型:
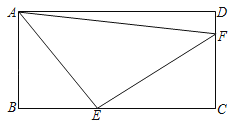
查看答案和解析>>【题目】如图,在长方形ABCD中,点E在BC上,点F在CD上,且满足BE=CF=a,AB=EC=b.
(1)判断△AEF的形状,并证明你的结论;
(2)请用含a,b的代数式表示△AEF的面积;
(3)当△ABE的面积为24,BC长为14时,求△ADF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.
 C.3D.
C.3D.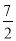
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
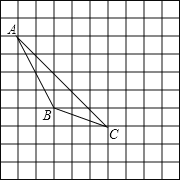
查看答案和解析>>【题目】如图,每个小正方形的边长均为1,每个小方格的顶点叫格点
(1)画出△ABC中AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是:______;
(4)S△ABC的面积是______.
相关试题

