【题目】如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G.若G是CD的中点,则BC的长是__________.

参考答案:
【答案】10.5
【解析】
利用ASA定理证明△EDG≌△FCG,从而求得DE=CF,EG=GF=![]() ,根据矩形的性质,设BC=x,则DE=x-6,DG=6,BF=2x-6,根据垂直平分线的性质求得EG=
,根据矩形的性质,设BC=x,则DE=x-6,DG=6,BF=2x-6,根据垂直平分线的性质求得EG=![]() ,然后根据勾股定理列方程求解即可.
,然后根据勾股定理列方程求解即可.
解:在矩形ABCD中,AD=BC,AB=CD=12,∠D=∠DCF=90°
∵G为CD中点,∴DG=CG
又∵∠EGD=∠FGC
∴△EDG≌△FCG
∴DE=CF,EG=GF=![]()
设BC=x,则DE=AD-AE=BC-AE=x-6,DG=CG=![]() =6,BF=BC+CF=BC+DE=2x-6,
=6,BF=BC+CF=BC+DE=2x-6,
又∵BE的垂直平分线交BC的延长线于点F,
∴EG=GF=![]()
∴在Rt△EDG中,![]()
解得:x=10.5
则BC的长是10.5
故答案为:10.5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形纸片ABC中,AD⊥BC与点D,BC=2,AD=
 ,沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形中较长对角线的长为__________.
,沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形中较长对角线的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象的顶点坐标为(1,
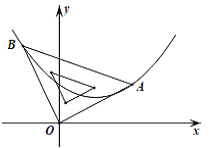
 ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).(1)求该二次函数的表达式;
(2)判断点B是否在此二次函数的图象上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图①中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图②的方式拼成一个长方形.
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中每个小正方形边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
(1)画一个△ABC,使AC=
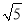 ,BC=
,BC=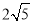 ,AB=5;
,AB=5;(2)若点D为AB的中点,则CD的长是 ;
(3)在(2)的条件下,直接写出点D到AC的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠BAC=90°,∠BAC和∠ABC的平分线交于点P
(1)如图1,在BC上取一点D,使得DB=AB,连接PD,△ABP与△DBP全等吗?为什么?
(2)在(1)的条件下,若DP=DC,则BC=AB+AP是否成立?请说明理由;
(3)如图2,在AC上取一点E,使得AE=AB,连接PE、PC,若∠ABC=60°,求∠EPC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)

相关试题

