【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73) 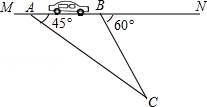
参考答案:
【答案】解:此车没有超速. 理由:过C作CH⊥MN,
∵∠CBN=60°,BC=200米,
∴CH=BCsin60°=200× ![]() =100
=100 ![]() (米),
(米),
BH=BCcos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100 ![]() 米,
米,
∴AB=100 ![]() ﹣100≈73(m),
﹣100≈73(m),
∵60千米/小时= ![]() m/s,
m/s,
∴ ![]() =14.6(m/s)<
=14.6(m/s)< ![]() ≈16.7(m/s),
≈16.7(m/s),
∴此车没有超速.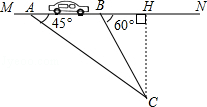
【解析】根据题意结合锐角三角函数关系得出BH,CH,AB的长进而求出汽车的速度,进而得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在ABCD中,点E,F在对角线BD上,且BE=DF,
求证:(1)AE=CF;(2)四边形AECF是平行四边形.
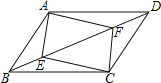
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉嘉在电脑上设计了一个有理数的运算程序:输入a,加*键,再输入b,得到运算a*b=(a2-b2)÷(a-b) .
(1)求(-2)*
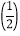 *
* 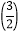 的值;
的值; (2)琪琪在运用此程序计算时,屏幕上显示“该程序无法操作”,请你运用所学的数学知识猜想一下,琪琪在输入数据时,可能出现什么情况?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了绝对值和有理数大小比较的知识后,老师在黑板上(如图所示)布置了作业,请完成.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB.
(1)用没有刻度的直尺和圆规按所给的要求作图:点C在线段BA的延长线上,且CA=AB;
(2)在(1)中,如果AB=28 cm,线段BC上有一点M,且线段AM∶BM=1∶3,求线段CM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

相关试题

