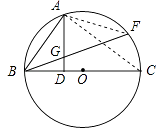
【题目】如图所示,BC是圆O的直径,点A,F在圆O上,连接AB,BF. 
(1)如图1,若点A、F把半圆三等分,连接OA,OA与BF交于点E.求证:E为OA的中点;
(2)如图2,若点A为弧 ![]() 的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
参考答案:
【答案】
(1)证明:∵A、F为半圆三等分点,
∴∠AOB= ![]() ×180°=60°,
×180°=60°,
∵OA=OB,
∴△OAB为等边三角形.
∵A为弧BF中点,
∴OA⊥BF,
∴BE平分OA,
∴E为OA中点
(2)证明:连接AF,AC,
∵A为弧BF中点,
∴ ![]() =
= ![]() ,
,
∴∠ABF=∠F.
∵ ![]() =
= ![]() ,
,
∴∠C=∠F,
∴∠C=∠ABF.
∵BC为圆O的直径,
∴∠BAC=90°,
∴∠BAD+∠CAD=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠ABG=∠BAG,
∴AG=BG.
【解析】(1)先求出∠AOB的度数,故可判断出△OAB为等边三角形,再由A为弧BF中点可得出OA⊥BF,进而可得出结论;(2)连接AF,AC,根据弧相等可得出∠C=∠ABF,由圆周角定理可得出∠BAC=90°,再由直角三角形的性质得出∠ABG=∠BAG,进而可得出结论.
【考点精析】通过灵活运用圆心角、弧、弦的关系和圆周角定理,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(1)求这个二次函数的解析式;
(2)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(3)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量
单价
不超过12 m3的部分
a元∕m3
超过12 m3但不超过20 m3的部分
1.5a元∕m3
超过20 m3的部分
2a元∕m3
(1) 当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2) 设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费_____________元(用含a、n的整式表示);
(3) 当a=2时,甲、乙两用户一个月共用水40 m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1 . 设CB1交AB于点D,A1B1分别交AB,AC于点E,F.

(1)求证:△BCD≌△A1CF;
(2)若旋转角ɑ为30°,
①请你判断△BB1D的形状;
②求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:

(1)2018在第________行,第________列;
(2)由五个数组成的“
 ”中:
”中:① 这五个数的和可能是2019吗,为什么?
② 如果这五个数的和是60,直接写出这五个数;
(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是圆O的内接四边形,BC是圆O的直径,∠ACB=20°,D为弧
 的中点,求∠DAC的度数.
的中点,求∠DAC的度数. 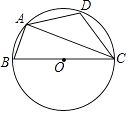
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

相关试题

