【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

参考答案:
【答案】(1)详见解析;(2)详见解析
【解析】试题分析:(1)根据平行四边形的性质、等腰三角形的性质,利用全等三角形的判定定理SAS可以证得△ADC≌△ECD;
(2)利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(对边平行且相等是四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
 ,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴ADCE是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,BC是圆O的直径,点A,F在圆O上,连接AB,BF.

(1)如图1,若点A、F把半圆三等分,连接OA,OA与BF交于点E.求证:E为OA的中点;
(2)如图2,若点A为弧 的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:

(1)2018在第________行,第________列;
(2)由五个数组成的“
 ”中:
”中:① 这五个数的和可能是2019吗,为什么?
② 如果这五个数的和是60,直接写出这五个数;
(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是圆O的内接四边形,BC是圆O的直径,∠ACB=20°,D为弧
 的中点,求∠DAC的度数.
的中点,求∠DAC的度数. 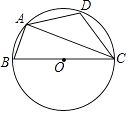
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
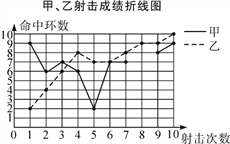
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
乙
1
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2018=0,O为原点
(1) 试求a和b的值
(2) 点C从O点出发向右运动,经过3秒后点C到A点的距离是点C到B点距离的3倍,求点C的运动速度?
(3) 点D以1个单位每秒的速度从点O向右运动,同时点P从点A出发以5个单位每秒的速度向左运动,点Q从点B出发,以20个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问
 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按如图所示方式搭图形,按照这种方式搭下去,搭第9个图形需火柴棒的根数是( )

A. 48 B. 54 C. 60 D. 以上都不对
相关试题

