【题目】已知二次函数y= x2+bx+c的图象经过点A（﹣3，6），并与x轴交于点B（﹣1，0）和点C，与y轴交于点E，顶点为P，对称轴与x轴交于点D
（1）求这个二次函数的解析式；
（2）连接CP，△DCP是什么特殊形状的三角形？并加以说明；
（3）点Q是第一象限的抛物线上一点，且满足∠QEO=∠BEO，求出点Q的坐标．

参考答案：

【答案】
（1）

解：把A（﹣3，6），B（﹣1，0）代入y= x2+bx+c，

得到 ，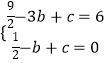

解得 ，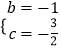

∴二次函数解析式为y= x2﹣x﹣ ．


（2）

解：结论：△DCP是等腰直角三角形．

理由：对于抛物线y= x2﹣x﹣ ，令y=0，则 x2﹣x﹣ =0，解得x=﹣1或3，

∴点C坐标（3，0），

令x=0则y=﹣ ，

∴点E坐标（0，﹣ ），

∵y= x2﹣x﹣ = （x﹣1）2﹣2，

∴顶点P坐标（1，﹣2），点D坐标（1，0），

∴CD=PD=2，

∵∠PDC=90°，

∴△PDC是等腰直角三角形．


（3）

解：如图，连接BE、DE．

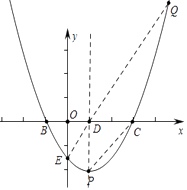
∵B（﹣1，0），D（1，0），E（0，﹣ ），

∴OB=OD，OE=OE，∠BOE=∠DOE，

∴△EOB≌△EOD，

∴∠DEO=∠BEO，

∴直线DE与抛物线的交点即为所求的点Q．

设直线DE的解析式为y=kx+b，则有 ，

解得 ，

∴直线DE的解析式为y= x﹣ ，

由 解得 或 ，

∴点Q坐标为（5，6）


【解析】（1）把A（﹣3，6），B（﹣1，0）代入y= x2+bx+c，解方程组即可解决问题．（2）结论：△DCP是等腰直角三角形．求出C、D、E三点坐标即可解决问题．（3）如图，连接BE、DE．只要证明△EOB≌△EOD，得到∠DEO=∠BEO，所以直线DE与抛物线的交点即为所求的点Q．求出直线DE的解析式，解方程组即可．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．

关闭