【题目】如图:矩形ABCD中AB=2,BC= ![]() ,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=度.
,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=度. 
参考答案:
【答案】60或120
【解析】解:
∵⊙A是以A为圆心,半径r=1的圆,AB=2,
∴当圆在矩形内部时,则与AD、BC都相切,
设与BC的切点为E,此时圆心为A′,连接A′E、A′B,如图,
则在Rt△A′BE中,A′E=1,A′B=AB=2,
∴∠A′BE=30°,
∴∠A′BA=90°﹣30°=60°;
当圆在矩形外部与BC相切时,设圆心为A″,
同理可求得∠A″BE=30°,
∴∠A″BA=90°+30°=120°;
综上可知α=60°或120°,
所以答案是:60或120.
【考点精析】根据题目的已知条件,利用矩形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间的函数关系图像.根据图像回答下列问题:

(1)小明到达离家最远的地方需________小时,此时离家________千米;
(2)小明出发2个小时后离家________千米;
(3)小明出发________小时后离家12千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )

A. P B. R C. Q D. T
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,△ABC的位置如图所示.
(1)你能想办法求出△ABC的面积吗?
(2)将△ABC向右平移6个单位,再向下平移2个单位,请在图中作出平移后的△A′B′C′,并写出△A′B′C′各顶点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师要为他家的长方形餐厅(如图1)选择一张餐桌,并且想按如下要求摆放:餐桌一侧靠墙,靠墙对面的桌边留出宽度不小于80 cm的通道,另两边各留出宽度不小于60 cm的通道.那么在图2的四张餐桌中,其规格符合要求的餐桌编号是________.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:计算1+2+22+23+24+…+22017+22018.
解:设S=1+2+22+23+24+…+22017+22018,①
将等式两边同时乘2,得
2S=2+22+23+24+25+…+22018+22019,②
由②-①,得2S-S=22019-1,即S=22019-1,即1+2+22+23+24+…+22017+22018=22019-1.
请你仿照此法回答下列问题:
(1)填空:1+2+22+23=________;
(2)计算:1+2+22+23+24+…+29+210;
(3)计算:1+
 +(
+( )2+(
)2+( )3+(
)3+( )4+…+(
)4+…+( )n(其中n为正整数).
)n(其中n为正整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是
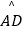 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°.
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°. 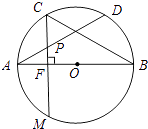
(1)求∠ABC的度数;
(2)若CM=4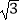 ,求
,求 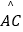 的长度.(结果保留π)
的长度.(结果保留π)
相关试题

