Question

【题目】如图，在⊙O中，AB是直径，点D是⊙O上的一点，点C是 的中点，弦CM垂直AB于点F，连接AD，交CF于点P，连接BC，∠DAB=30°．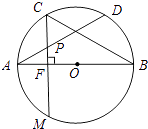

（1）求∠ABC的度数；
（2）若CM=4 ，求 的长度．（结果保留π）

Answer 1

【答案】
（1）解：如图，连接BD，

∵AB为⊙O的直径，

∴∠ADB=90°，

∵∠DAB=30°，

∴∠ABD=90°﹣30°=60°．

∵C是 的中点，

∴∠ABC=∠DBC= ∠ABD=30°

（2）解：如图，连接OC，则∠AOC=2∠ABC=60°，

∵CM⊥直径AB于点F，

∴CF= CM=2 ．

∴在Rt△COF中，CO= CF= ×2 =4，

∴ 的长度为 = ．

【解析】（1）连接BD，根据AB为⊙O的直径，求出∠ADB=90°，得到∠ABD=60°，再根据C是 的中点，求出∠ABC的度数；（2）连接OC，则∠AOC=2∠ABC=60°，求出CO的长，即可求出 的长度．
【考点精析】解答此题的关键在于理解垂径定理的相关知识，掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧，以及对圆心角、弧、弦的关系的理解，了解在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．