【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
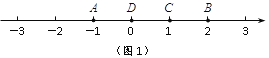
知识运用:
⑴ 如图1,点B是(D,C)的好点吗? (填是或不是);
⑵ 如图2,A、B为数轴上两点,点A所表示的数为-40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

参考答案:
【答案】(1)是;(2)10或20或15
【解析】
(1)计算B到D的距离,B到C的距离,看是否满足好点的定义;
(2)分四种情况讨论:(Ⅰ)P是【A,B】的好点;(Ⅱ)若P是【B,A】的好点;(Ⅲ)若B是【A,P】的好点;(Ⅳ)若A是【B,P】的好点,根据好点的定义列出方程求解.
解:⑴ 由图可得,BD=2,BC=1,BD=2BC,所以点B是【D,C】的好点.
⑵(Ⅰ)若P是【A,B】的好点,则AP=2BP 可得BP=20,2t=20,t=10;
(Ⅱ)若P是【B,A】的好点,则BP=2AP 可得BP=40,2t=40,t=20;
(Ⅲ)若B是【A,P】的好点,则BA=2BP 可得BP=30,2t=30,t=15;
(Ⅳ)若A是【B,P】的好点,则AB=2AP 可得AP=30,BP=30 2t=15,t=15;
综上所述:当t=10、20、15时,P、A和B中恰有一个点为其余两点的好点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】手机给学生带来方便的同时也带来了很大的影响.新化县某校初一年级在一次家长会上对若干家长进行了一次对“学生使用手机”现象看法的调查,将调查数据整理得如下统计图(
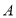 :绝对弊大于利,
:绝对弊大于利,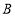 :绝对利大于弊,
:绝对利大于弊, :相对弊大于利,
:相对弊大于利, :相对利大于弊):
:相对利大于弊):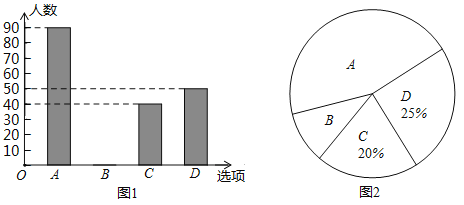
(1)这次调查的家长总人数为多少人?
(2)本次调查的家长中表示“
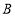 绝对利大于弊”所占的百分比是多少?并补全条形统计图.
绝对利大于弊”所占的百分比是多少?并补全条形统计图.(3)求扇形统计图图2中表示“
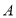 :绝对弊大于利”的扇形的圆心角度数.
:绝对弊大于利”的扇形的圆心角度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
③连接FC.
(2)猜想与证明:猜想四边形ABCF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为
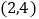 ,点E的坐标为
,点E的坐标为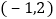 ,则点P的坐标为______.
,则点P的坐标为______.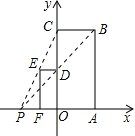
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=8,BC=5,以点A为圆心,以任意长为半径作弧,分别交AD、AB于点P、Q,再分别以P、Q为圆心,以大于
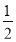 PQ的长为半径作弧,两弧在∠DAB内交于点M,连接AM并延长交CD于点E,则CE的长为( )
PQ的长为半径作弧,两弧在∠DAB内交于点M,连接AM并延长交CD于点E,则CE的长为( )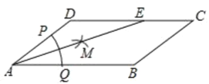
A. 3B. 5C. 2D. 6.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面说法中正确的个数有( )
①等腰三角形的高与中线重合
②一组对边平行,另一组对边相等的四边形是平行四边形
③顺次连接任意四边形的中点组成的新四边形为平行四边形
④七边形的内角和为900°,外角和为360°
⑤如果方程
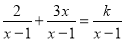 会产生增根,那么k的值是4
会产生增根,那么k的值是4A. 1个B. 2个C. 3个D. 4个
相关试题

