【题目】下面说法中正确的个数有( )
①等腰三角形的高与中线重合
②一组对边平行,另一组对边相等的四边形是平行四边形
③顺次连接任意四边形的中点组成的新四边形为平行四边形
④七边形的内角和为900°,外角和为360°
⑤如果方程![]() 会产生增根,那么k的值是4
会产生增根,那么k的值是4
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】B
【解析】
依据等腰三角形的性质可对①做出判断,依据平行四边形的判定定理可对②做出判断;依据三角形的中位线定理和平行四边形的判定定理可对③做出判断;依据多边形的内角和公式可对④做出判断,依据方程有增跟可得到x得值,然后将分式方程化为整式方程,最后,将x的值代入求得k的值即可.
解:①等腰三角形的底边上的高与底边上中线重合,故①错误;
②一组对边平行,另一组对边相等的四边形还可能是等腰梯形,故②错误;
③顺次连接任意四边形各边中点得到的四边形,这个四边形的对边都等于原来四边形与这组对边相对的对角线的一半,并且和这条对角线平行,故得到的中点四边形是平行四边形,故③正确.
④七边形的内角和=(7-2)×180°=900°,任意多边形的外角和都等于360°,故④正确;
⑤如果方程![]() 会产生增根,那么x-1=0,解得:x=1.
会产生增根,那么x-1=0,解得:x=1.
![]() ,
,
∴2+3x=k,
将x=1代入得:k=2+3×1=5,故⑤错误.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
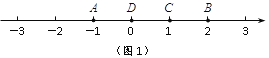
知识运用:
⑴ 如图1,点B是(D,C)的好点吗? (填是或不是);
⑵ 如图2,A、B为数轴上两点,点A所表示的数为-40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=8,BC=5,以点A为圆心,以任意长为半径作弧,分别交AD、AB于点P、Q,再分别以P、Q为圆心,以大于
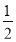 PQ的长为半径作弧,两弧在∠DAB内交于点M,连接AM并延长交CD于点E,则CE的长为( )
PQ的长为半径作弧,两弧在∠DAB内交于点M,连接AM并延长交CD于点E,则CE的长为( )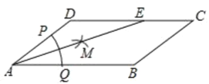
A. 3B. 5C. 2D. 6.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4,AD=9点F是边BC上的一点,点E是AD上的一点,AE:ED=1:2,连接EF、DF,若EF=2
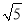 ,则CF的长为______________。
,则CF的长为______________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若a+b=2,则称a与b是关于1的平衡数.
(1)直接填写:①3与_ 是关于1的平衡数: :
②1-x与________是关于 1的平衡数(用含x的代数式表示);
(2)若
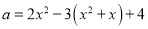 ,
,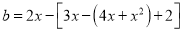 ,先化简a. b,再判断a与b是否是关于1的平衡数.
,先化简a. b,再判断a与b是否是关于1的平衡数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:

根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为 ;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有 人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率.
相关试题

